Question

Calculate CFSE of the following complex:
${{\left[ Co{{F}_{6}} \right]}^{3-}}$
(A) −0.4 ${{\Delta }_{o}}$
(B) 0.4 ${{\Delta }_{o}}$
(C) −0.4 ${{\Delta }_{t}}$
(D) 0.6 ${{\Delta }_{t}}$

Answer 1

The given complex is characterized by a smaller crystal field. As a result, instead of pairing with another electron, electrons choose to occupy the higher d orbitals. From this we can calculate the number of electrons in different orbitals and it will give us the value of CFSE.

Complete step by step solution:
- According to crystal field theory, an octahedral complex which has six ligands systematically arranged around a central atom. Hence, we can assume that the given complex ${{\left[ Co{{F}_{6}} \right]}^{3-}}$is an octahedral complex.
- In an octahedral complex, the d orbitals are split into ${{t}_{2g}}$ and ${{e}_{g}}$.Here the ${{t}_{2g}}$ orbitals will be lower in energy compared to ${{e}_{g}}$orbitals. The splitting can be shown as follows,

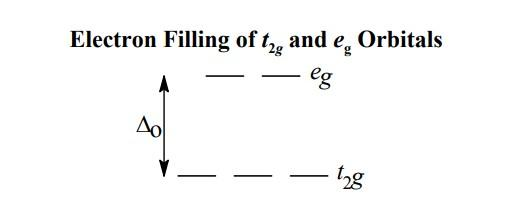
- Let's find the oxidation state of cobalt(x) in ${{\left[ Co{{F}_{6}} \right]}^{3-}}$.We know fluorine has a charge of −1.
$x-6=-3$
∴ $x$=+3
Thus, Co exists as $C{{o}^{3+}}$. Its outer electronic configuration can be given as$3d{{ }^{6}}4{{s}^{0}}$. The arrangement of these 3d electrons will determine the crystal field stabilization energy (CFSE). There are two possible fillings in the ${{t}_{2g}}$ and ${{e}_{g}}$ orbitals for electronic configuration from ${{d}^{4}}$ to ${{d}^{7}}$ .
- There is a high spin configuration which minimizes the pairing of electrons by spreading them across the two orbitals and there is a low spin configuration which minimizes the occupancy of electrons in ${{e}_{g}}$ by the pairing of electrons in ${{t}_{2g}}$itself.
- CFSE of an octahedral complex is given by,
CFSE =$\left( -0.4\times n{{t}_{2g}} \right)+(0.6n{{e}_{g}}){{\Delta }_{o}}$
Where $n{{t}_{2g}}$ is the number of electrons occupied in ${{t}_{2g}}$ orbital and $n{{e}_{g}}$ is the number of electrons occupied in ${{e}_{g}}$ orbital.
- From the spectrochemical series it's clear that ${{F}^{-}}$is a weak field ligand and thus it will give rise to the high spin complex. Therefore, the electrons will spread in both orbitals giving rise to the configuration of ${{t}^{4}}_{2g}{{e}^{2}}_{g}$. This implies that there are four electrons in ${{t}_{2g}}$ orbital and two in ${{e}_{g}}$orbital. Thus, CFSE can be found as follows
CFSE = (−0.4×4) +(0.6×2)
= −1.6+1.2
= −0.4 ${{\Delta }_{o}}$
Therefore, the answer is option (A) −0.4${{\Delta }_{o}}$.

Note: As we mentioned above, the spectrochemical series plays an important role in determining whether the complex is high spin or low spin. It can be represented as follows
${{I}^{-}}<~B{{r}^{-}}<~C{{l}^{-}}<~{{F}^{-}}<~O{{H}^{-}}<~{{C}_{2}}O_{4}^{2-}<~{{H}_{2}}O<~N{{H}_{3}}<~en<~bipy<~phen<~C{{N}^{-}}\approx CO$. Ligands up to water are generally weak ligands and thus form high spin complexes and ligands beyond water are strong field ligands and they form low spin complexes.