Question
Question: The two circles x²+y²+2ax+c=0 and x²+y²+2by+c=0 touch if $\frac{1}{a^2}+\frac{1}{b^2}=$...
The two circles x²+y²+2ax+c=0 and x²+y²+2by+c=0 touch if a21+b21=
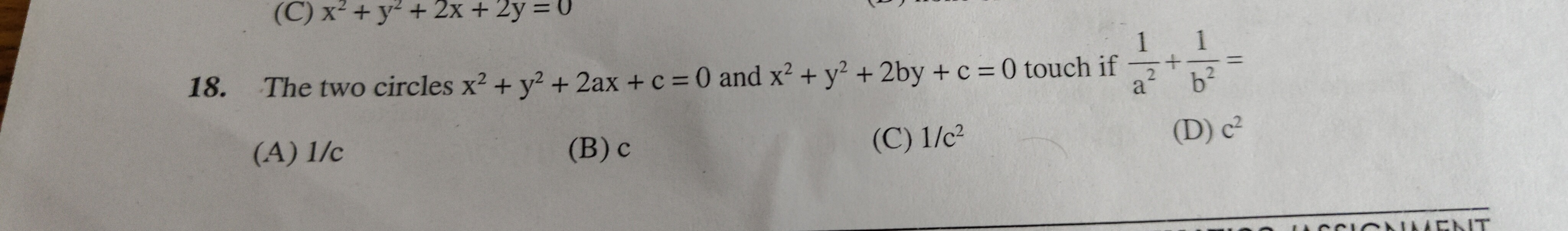
1/c
c
1/c²
c²
1/c
Solution
The equations of the two circles are given by: Circle 1: x2+y2+2ax+c=0 Circle 2: x2+y2+2by+c=0
The center and radius of a circle with the equation x2+y2+2gx+2fy+d=0 are (−g,−f) and g2+f2−d respectively.
For Circle 1: Center C1=(−a,0) Radius r1=a2−c
For Circle 2: Center C2=(0,−b) Radius r2=b2−c
The distance between the centers C1 and C2 is: d(C1,C2)=(0−(−a))2+(−b−0)2=a2+b2
For the two circles to touch, the distance between their centers must be equal to the sum or the absolute difference of their radii: d(C1,C2)=r1+r2 or d(C1,C2)=∣r1−r2∣
Squaring both sides: d(C1,C2)2=(r1±r2)2 a2+b2=(a2−c±b2−c)2 a2+b2=(a2−c)+(b2−c)±2(a2−c)(b2−c) a2+b2=a2+b2−2c±2(a2−c)(b2−c) 0=−2c±2(a2−c)(b2−c) 2c=±2(a2−c)(b2−c) c=±(a2−c)(b2−c)
Squaring both sides again: c2=(a2−c)(b2−c) c2=a2b2−a2c−b2c+c2 0=a2b2−a2c−b2c a2c+b2c=a2b2
Divide by a2b2c (assuming a,b,c=0): a2b2ca2c+a2b2cb2c=a2b2ca2b2 b21+a21=c1
Therefore, a21+b21=c1.
