Question

x^2-x+1>0

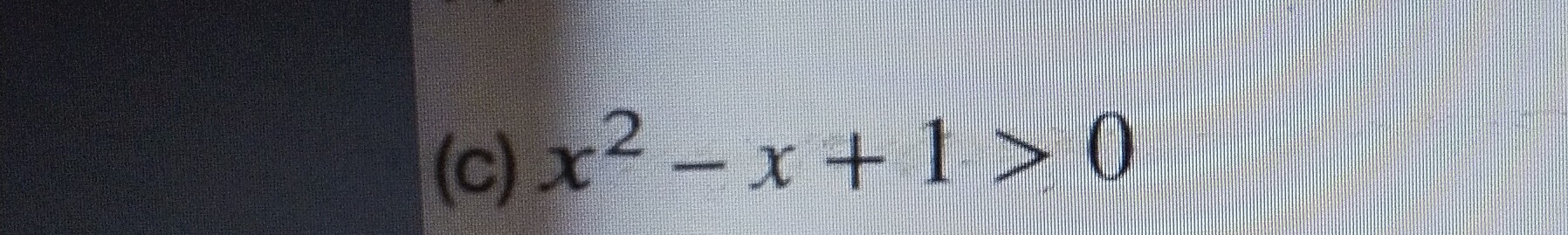
Answer 1

The solution set is $(-\infty, \infty)$.

Answer 2

The discriminant of the quadratic $x^2-x+1$ is $\Delta = (-1)^2 - 4(1)(1) = -3$. Since $\Delta < 0$ and the leading coefficient $a=1 > 0$, the quadratic $x^2-x+1$ is positive for all real values of $x$. Therefore, the inequality $x^2-x+1>0$ is true for all $x \in \mathbb{R}$.