Question

The equation of a progressive wave is given by, $y = 3 \sin \pi (\frac{t}{0.02}-\frac{x}{20})m$. Then the frequency of the wave is

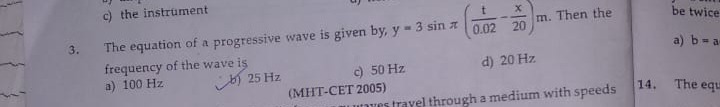
• A. 100 Hz
• B. 25 Hz
• C. 50 Hz
• D. 20 Hz

Answer 1

Answer: (B)

25 Hz

Answer 2

The wave equation is

$$y = 3 \sin\left[\pi\left(\frac{t}{0.02} - \frac{x}{20}\right)\right]$$

Rewrite the time term:

$$\frac{t}{0.02} = 50t$$

Thus, the argument becomes:

$$\pi \left(50t - \frac{x}{20}\right) = 50\pi\, t - \frac{\pi}{20}\, x$$

Here, the angular frequency $\omega = 50\pi$ rad/s.

The frequency is given by:

$$f = \frac{\omega}{2\pi} = \frac{50\pi}{2\pi} = 25\text{ Hz}$$