Solveeit Logo
Login

Question

Question: $\tan^2 36^{\circ} \tan^2 72^{\circ} = 5.$...

tan⁡236∘tan⁡272∘=5.\tan^2 36^{\circ} \tan^2 72^{\circ} = 5.

Answer

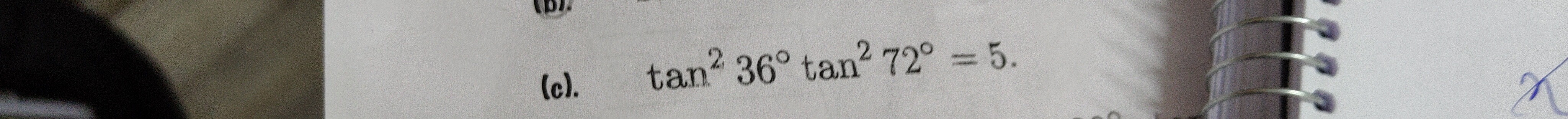
True

Explanation

Solution

The problem asks us to verify if the statement tan⁡236∘tan⁡272∘=5\tan^2 36^{\circ} \tan^2 72^{\circ} = 5 is true.

To verify this, we need to find the values of tan⁡236∘\tan^2 36^{\circ} and tan⁡272∘\tan^2 72^{\circ}.

Step 1: Calculate tan⁡236∘\tan^2 36^{\circ}

We know the value of cos⁡36∘\cos 36^{\circ}: cos⁡36∘=5+14\cos 36^{\circ} = \frac{\sqrt{5}+1}{4}

Now, we find sin⁡236∘\sin^2 36^{\circ} using the identity sin⁡2θ=1−cos⁡2θ\sin^2 \theta = 1 - \cos^2 \theta:

sin⁡236∘=1−(5+14)2=1−(5)2+12+2516=1−5+1+2516\sin^2 36^{\circ} = 1 - \left(\frac{\sqrt{5}+1}{4}\right)^2 = 1 - \frac{(\sqrt{5})^2 + 1^2 + 2\sqrt{5}}{16} = 1 - \frac{5+1+2\sqrt{5}}{16} =1−6+2516=16−(6+25)16=10−2516= 1 - \frac{6+2\sqrt{5}}{16} = \frac{16 - (6+2\sqrt{5})}{16} = \frac{10-2\sqrt{5}}{16}

Now, we can find tan⁡236∘=sin⁡236∘cos⁡236∘\tan^2 36^{\circ} = \frac{\sin^2 36^{\circ}}{\cos^2 36^{\circ}}:

tan⁡236∘=10−25166+2516=10−256+25\tan^2 36^{\circ} = \frac{\frac{10-2\sqrt{5}}{16}}{\frac{6+2\sqrt{5}}{16}} = \frac{10-2\sqrt{5}}{6+2\sqrt{5}}

To simplify this expression, we multiply the numerator and denominator by the conjugate of the denominator, which is 6−256-2\sqrt{5}:

tan⁡236∘=10−256+25×6−256−25=10(6)−10(25)−25(6)+25(25)62−(25)2\tan^2 36^{\circ} = \frac{10-2\sqrt{5}}{6+2\sqrt{5}} \times \frac{6-2\sqrt{5}}{6-2\sqrt{5}} = \frac{10(6) - 10(2\sqrt{5}) - 2\sqrt{5}(6) + 2\sqrt{5}(2\sqrt{5})}{6^2 - (2\sqrt{5})^2} =60−205−125+4(5)36−4(5)=60−325+2036−20=80−32516= \frac{60 - 20\sqrt{5} - 12\sqrt{5} + 4(5)}{36 - 4(5)} = \frac{60 - 32\sqrt{5} + 20}{36 - 20} = \frac{80 - 32\sqrt{5}}{16} tan⁡236∘=16(5−25)16=5−25\tan^2 36^{\circ} = \frac{16(5 - 2\sqrt{5})}{16} = 5 - 2\sqrt{5}

Step 2: Calculate tan⁡272∘\tan^2 72^{\circ}

We use the identity tan⁡72∘=tan⁡(90∘−18∘)=cot⁡18∘\tan 72^{\circ} = \tan (90^{\circ} - 18^{\circ}) = \cot 18^{\circ}. So, tan⁡272∘=cot⁡218∘=cos⁡218∘sin⁡218∘\tan^2 72^{\circ} = \cot^2 18^{\circ} = \frac{\cos^2 18^{\circ}}{\sin^2 18^{\circ}}.

We know the value of sin⁡18∘\sin 18^{\circ}: sin⁡18∘=5−14\sin 18^{\circ} = \frac{\sqrt{5}-1}{4}

Now, we find sin⁡218∘\sin^2 18^{\circ}:

sin⁡218∘=(5−14)2=(5)2+12−2516=5+1−2516=6−2516\sin^2 18^{\circ} = \left(\frac{\sqrt{5}-1}{4}\right)^2 = \frac{(\sqrt{5})^2 + 1^2 - 2\sqrt{5}}{16} = \frac{5+1-2\sqrt{5}}{16} = \frac{6-2\sqrt{5}}{16}

Next, we find cos⁡218∘\cos^2 18^{\circ} using cos⁡2θ=1−sin⁡2θ\cos^2 \theta = 1 - \sin^2 \theta:

cos⁡218∘=1−6−2516=16−(6−25)16=10+2516\cos^2 18^{\circ} = 1 - \frac{6-2\sqrt{5}}{16} = \frac{16 - (6-2\sqrt{5})}{16} = \frac{10+2\sqrt{5}}{16}

Now, we can find tan⁡272∘\tan^2 72^{\circ}:

tan⁡272∘=10+25166−2516=10+256−25\tan^2 72^{\circ} = \frac{\frac{10+2\sqrt{5}}{16}}{\frac{6-2\sqrt{5}}{16}} = \frac{10+2\sqrt{5}}{6-2\sqrt{5}}

To simplify this expression, we multiply the numerator and denominator by the conjugate of the denominator, which is 6+256+2\sqrt{5}:

tan⁡272∘=10+256−25×6+256+25=10(6)+10(25)+25(6)+25(25)62−(25)2\tan^2 72^{\circ} = \frac{10+2\sqrt{5}}{6-2\sqrt{5}} \times \frac{6+2\sqrt{5}}{6+2\sqrt{5}} = \frac{10(6) + 10(2\sqrt{5}) + 2\sqrt{5}(6) + 2\sqrt{5}(2\sqrt{5})}{6^2 - (2\sqrt{5})^2} =60+205+125+4(5)36−4(5)=60+325+2036−20=80+32516= \frac{60 + 20\sqrt{5} + 12\sqrt{5} + 4(5)}{36 - 4(5)} = \frac{60 + 32\sqrt{5} + 20}{36 - 20} = \frac{80 + 32\sqrt{5}}{16} tan⁡272∘=16(5+25)16=5+25\tan^2 72^{\circ} = \frac{16(5 + 2\sqrt{5})}{16} = 5 + 2\sqrt{5}

Step 3: Calculate the product tan⁡236∘tan⁡272∘\tan^2 36^{\circ} \tan^2 72^{\circ}

Now we multiply the values we found:

tan⁡236∘tan⁡272∘=(5−25)(5+25)\tan^2 36^{\circ} \tan^2 72^{\circ} = (5 - 2\sqrt{5})(5 + 2\sqrt{5})

This is in the form of (a−b)(a+b)=a2−b2(a-b)(a+b) = a^2 - b^2, where a=5a=5 and b=25b=2\sqrt{5}.

=52−(25)2=25−(4×5)=25−20=5= 5^2 - (2\sqrt{5})^2 = 25 - (4 \times 5) = 25 - 20 = 5

Thus, the statement tan⁡236∘tan⁡272∘=5\tan^2 36^{\circ} \tan^2 72^{\circ} = 5 is true.