Solveeit Logo
Login

Question

Question: The two vectors $\hat{j}+\hat{k}$ and $3\hat{i}-\hat{j}+4\hat{k}$ represent the two sides AB and AC ...

The two vectors j^+k^\hat{j}+\hat{k} and 3i^−j^+4k^3\hat{i}-\hat{j}+4\hat{k} represent the two sides AB and AC respectively of △ABC\triangle ABC. The length of the median through A is

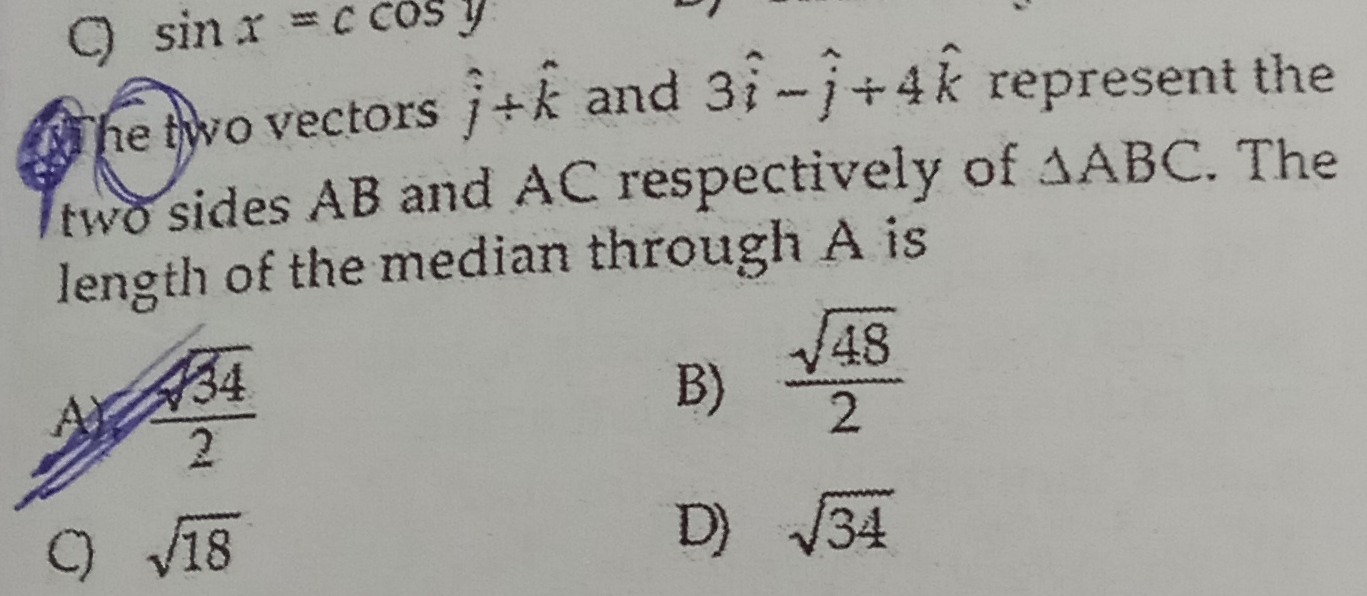
A

342\frac{\sqrt{34}}{2}

B

482\frac{\sqrt{48}}{2}

C

18\sqrt{18}

D

34\sqrt{34}

Answer

342\frac{\sqrt{34}}{2}

Explanation

Solution

Given the sides of triangle ABC as:

AB⃗=j^+k^\vec{AB} = \hat{j}+\hat{k} and AC⃗=3i^−j^+4k^\vec{AC}= 3\hat{i}-\hat{j}+4\hat{k}

The median from A goes to the midpoint M of BC. Since

AM⃗=AB⃗+AC⃗2\vec{AM} = \frac{\vec{AB} + \vec{AC}}{2}

we calculate:

AM⃗=(j^+k^)+(3i^−j^+4k^)2=3i^+0j^+5k^2=3i^+5k^2\vec{AM} = \frac{(\hat{j}+\hat{k}) + (3\hat{i}-\hat{j}+4\hat{k})}{2} = \frac{3\hat{i} +0\hat{j} +5\hat{k}}{2} = \frac{3\hat{i}+5\hat{k}}{2}

The length of the median is:

∣AM⃗∣=1232+02+52=129+25=342|\vec{AM}| = \frac{1}{2}\sqrt{3^2 + 0^2 + 5^2} = \frac{1}{2}\sqrt{9+25} = \frac{\sqrt{34}}{2}