Question

Two beads of mass m and 2m are connected by a massless rod of length R and threaded onto a smooth circular wire of radius R. When the wire rotates uniformly with angular velocity $\omega$ about a vertical diameters, the beads do not slide on it and rod remains vertical as shown. What must be the angular velocity $\omega$ of the wire? (Take R = 15 m)

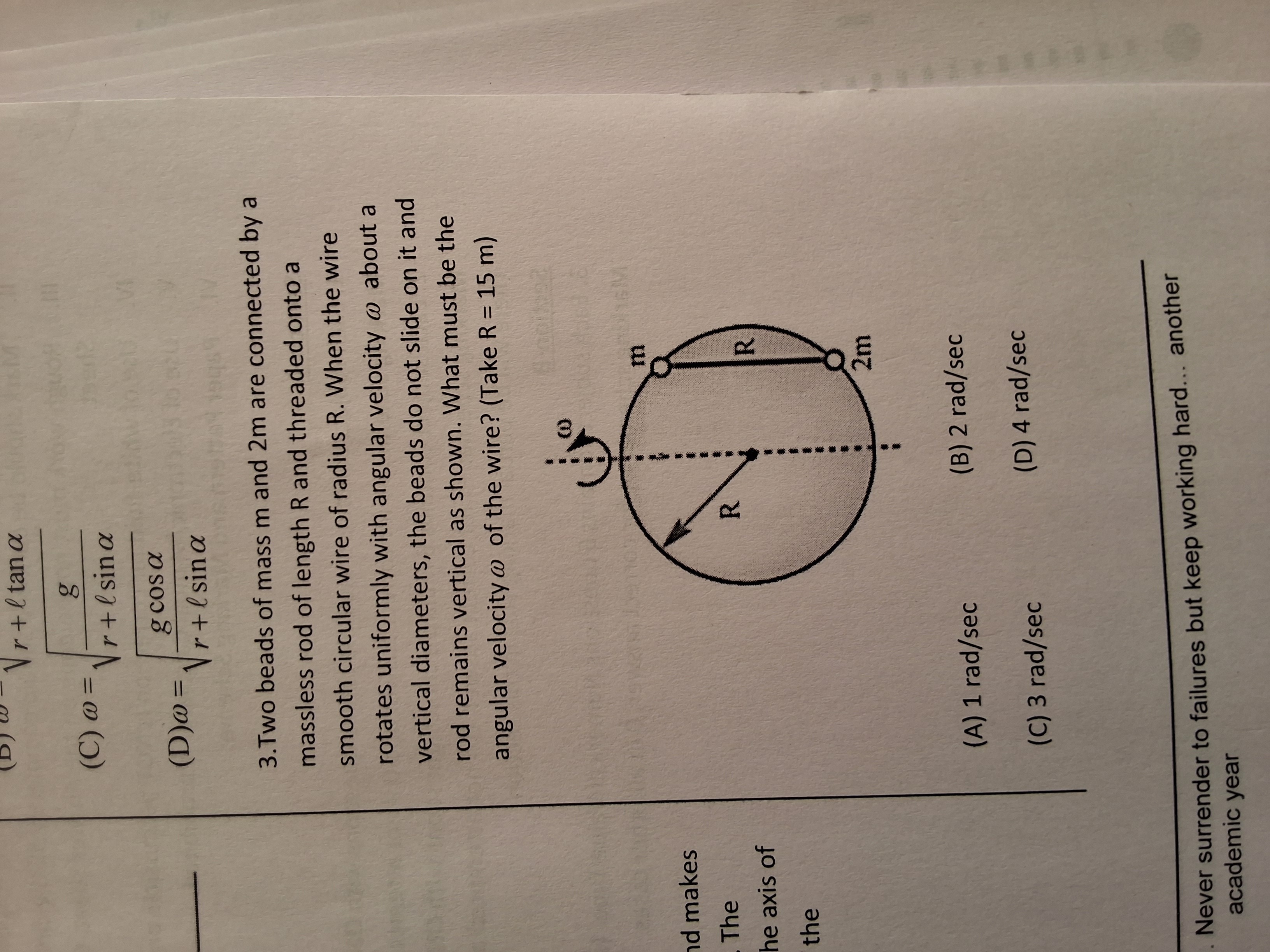
• A. 1 rad/sec
• B. 2 rad/sec
• C. 3 rad/sec
• D. 4 rad/sec

Answer 1

Answer: (B)

2 rad/sec

Answer 2

The angular velocity $\omega$ of the wire must be 2 rad/sec.

Explanation of the solution:

1. Determine the positions of the beads on the circular wire. Given a vertical rod of length R connecting two beads on a circle of radius R, the beads must be at heights $z = R/2$ (for mass m, $\theta = 60^\circ$) and $z = -R/2$ (for mass 2m, $\theta = 120^\circ$). The horizontal distance from the axis of rotation for both beads is $r = R\sin\theta = R\sqrt{3}/2$.
2. Apply the condition for no sliding: The net force component along the tangent to the wire must be zero for each bead.
   • For the upper bead (m): Tangential component of forces (weight, centrifugal force, rod force T) sum to zero. This yields $T = m(g + \omega^2 R/2)$.
   • For the lower bead (2m): Similarly, tangential components sum to zero. This yields $T = m\omega^2 R - 2mg$.
3. Equate the two expressions for T: $m(g + \omega^2 R/2) = m\omega^2 R - 2mg$.
4. Solve for $\omega$: This simplifies to $3g = \omega^2 R/2$, leading to $\omega = \sqrt{6g/R}$.
5. Substitute $R = 15$ m and $g = 10$ m/s$^2$ into the formula to get $\omega = \sqrt{6 \times 10 / 15} = \sqrt{4} = 2$ rad/sec.