Question
Question: The domain of the function $f(x) = \sin^{-1}\{\log_2(\frac{1}{2}x^2)\}$ is...
The domain of the function f(x)=sin−1{log2(21x2)} is
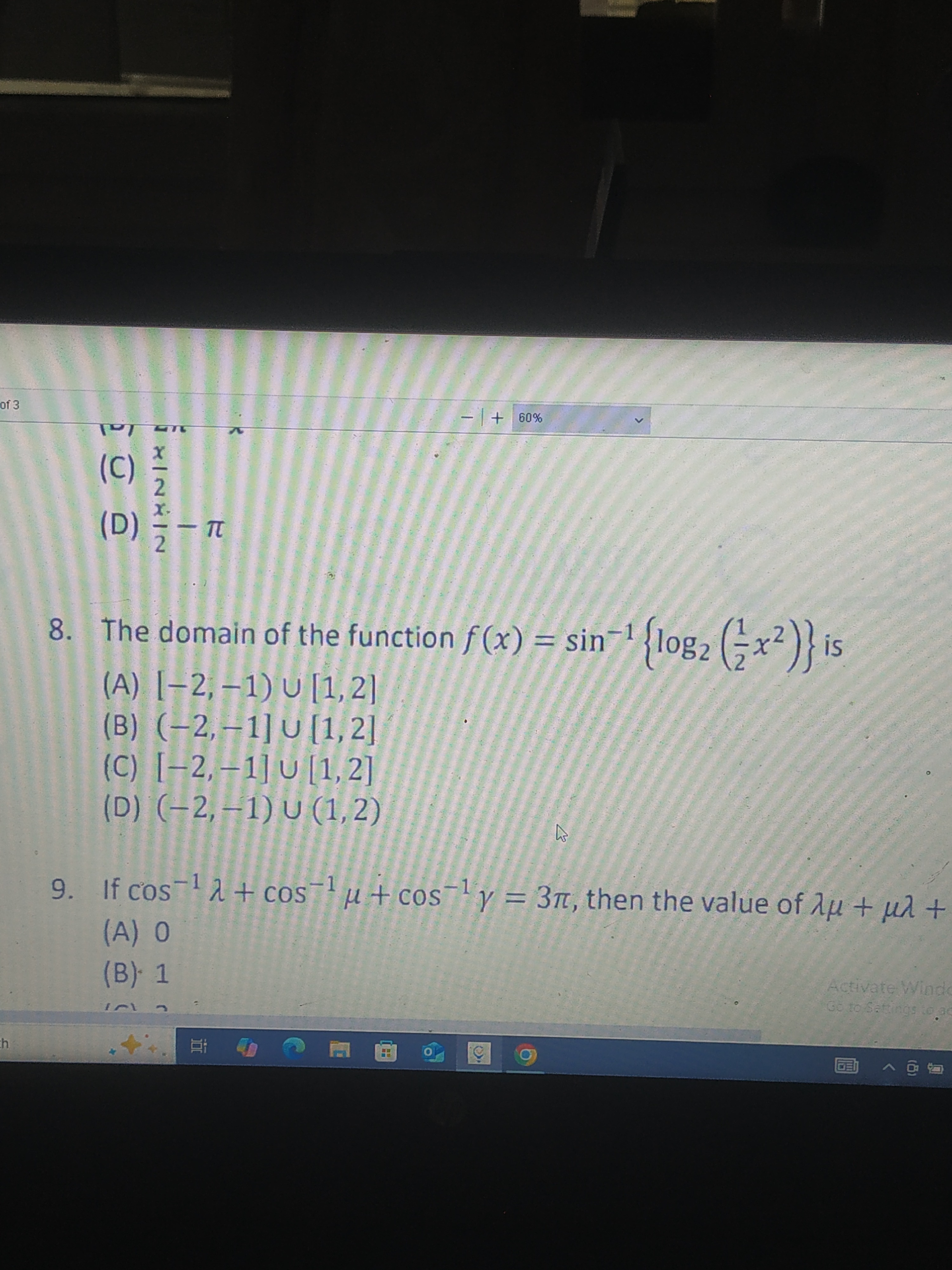
[-2, -1) ∪ [1, 2]
(-2, -1] ∪ [1, 2]
[-2, -1] ∪ [1, 2]
(-2, -1) ∪ (1, 2)
[-2, -1] ∪ [1, 2]
Solution
For the function f(x)=sin−1{log2(21x2)} to be defined, two conditions must be met:
-
Domain of sin−1(u): The argument u must lie in the interval [−1,1]. Here, u=log2(21x2). So, we must have: −1≤log2(21x2)≤1
-
Domain of logb(v): The argument v must be strictly positive. Here, v=21x2. So, we must have: 21x2>0⟹x2>0⟹x=0
Now, let's solve the inequality from condition 1: −1≤log2(21x2)≤1 Since the base of the logarithm is 2 (which is greater than 1), we can convert the logarithmic inequalities to exponential inequalities without changing the direction of the inequality signs: 2−1≤21x2≤21 21≤21x2≤2 This can be split into two separate inequalities:
-
Inequality 1: 21≤21x2 Multiply both sides by 2: 1≤x2 x2≥1 This implies x≤−1 or x≥1. In interval notation, x∈(−∞,−1]∪[1,∞).
-
Inequality 2: 21x2≤2 Multiply both sides by 2: x2≤4 This implies −2≤x≤2. In interval notation, x∈[−2,2].
To satisfy both inequalities simultaneously, we need to find the intersection of their solution sets: ((−∞,−1]∪[1,∞))∩[−2,2] This intersection is [−2,−1]∪[1,2].
Finally, we must also satisfy condition 2, which states x=0. The interval [−2,−1]∪[1,2] does not include 0, so this condition is already satisfied.
Therefore, the domain of the function f(x) is [−2,−1]∪[1,2].
