Question

The negation of the statement $(p \land q) \rightarrow (\sim p \lor r)$ is [2023]

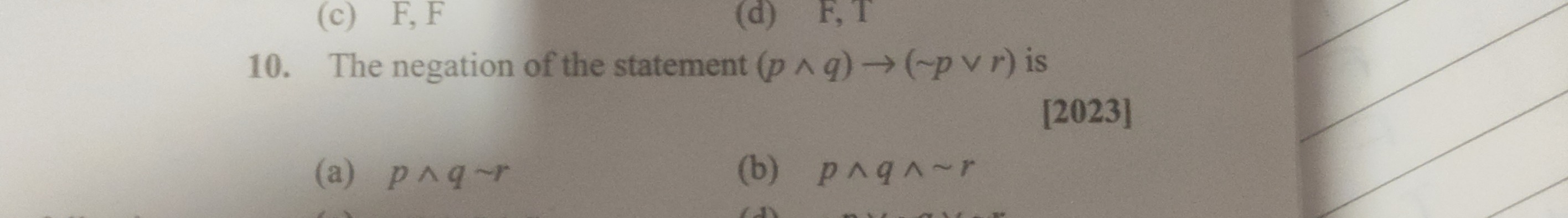
• A. $p \land q \land \sim r$
• B. $p \land q \land \sim r$

Answer 1

Answer: (A), (B)

$p\land q\land\sim r$ (Both options (a) and (b) yield the same correct result.)

Answer 2

To negate an implication, we use the equivalence

$\neg (A\to B) \equiv A\land\neg B$.

Here, $A \equiv (p\land q)$ and $B \equiv (\sim p\lor r)$. Thus,

$\neg((p\land q)\to (\sim p\lor r)) = (p\land q)\land\neg(\sim p\lor r)$.

Now, apply De Morgan's law to $\neg(\sim p\lor r)$:

$\neg(\sim p\lor r) = p\land\sim r$.

So, combining we get:

$(p\land q)\land (p\land\sim r) = p\land q\land\sim r$.