Question

The negation of the statement pattern $\sim s \vee (\sim r \wedge s)$ is [2023] equivalent to

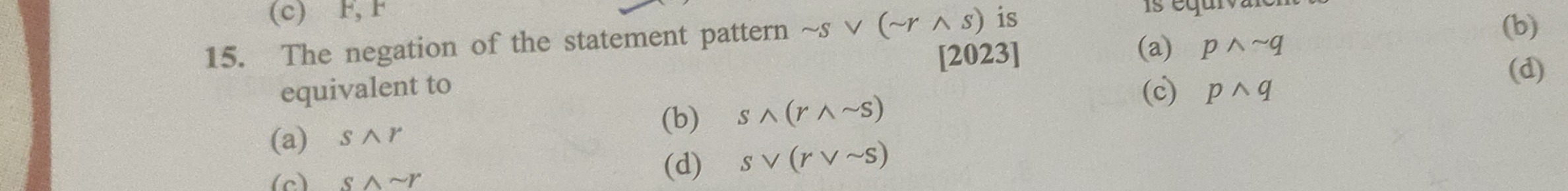
• A. $s \wedge r$
• B. $s \wedge (r \wedge \sim s)$
• C. $s \wedge \sim r$
• D. $s \vee (r \vee \sim s)$

Answer 1

Answer: (A)

$s \wedge r$

Answer 2

Given the statement

$$\sim s \vee (\sim r \wedge s)$$

we need to find its negation.

1. Negate the statement using De Morgan's law:

$$\neg\left[\sim s \vee (\sim r \wedge s)\right] = \neg(\sim s) \wedge \neg(\sim r \wedge s)$$

2. Simplify each part:

• $\neg(\sim s) = s$
• $\neg(\sim r \wedge s) = \neg(\sim r) \vee \neg s = r \vee \neg s$

So, we have:

$$s \wedge (r \vee \neg s)$$

3. Distribute and simplify:

$$s \wedge (r \vee \neg s) = (s \wedge r) \vee (s \wedge \neg s)$$

But $s \wedge \neg s$ is always false, hence the expression simplifies to:

$$s \wedge r$$

Thus, the negation is equivalent to $s \wedge r$.