Question
Question: Let P(a,b) be a point in the first quadrant. Two circles are drawn through P touching the co-ordinat...
Let P(a,b) be a point in the first quadrant. Two circles are drawn through P touching the co-ordinate axes. If one circle bisects the circumference of other, then possible values of ba - is/are-
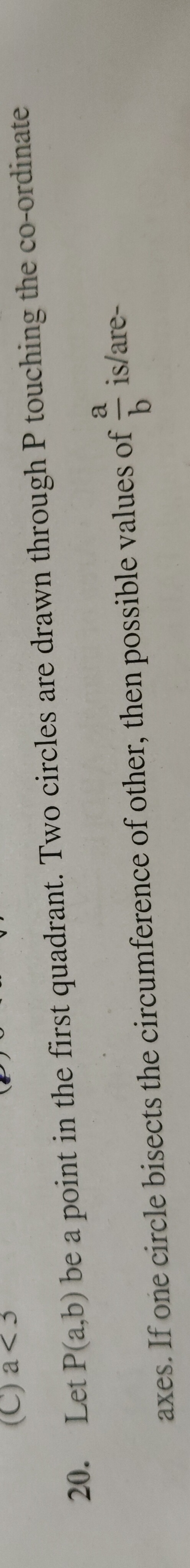
a² - 6ab + b² = 0
a² - 4ab + b² = 0
a² + 6ab + b² = 0
a² + 4ab + b² = 0
a² - 6ab + b² = 0
Solution
The equation of a circle touching the coordinate axes in the first quadrant with radius r is (x−r)2+(y−r)2=r2. If P(a,b) lies on this circle, then (a−r)2+(b−r)2=r2, which simplifies to r2−2(a+b)r+(a2+b2)=0. Let the radii of the two circles be r1 and r2. Then r1 and r2 are the roots of this quadratic equation. By Vieta's formulas, r1+r2=2(a+b) and r1r2=a2+b2.
The condition that one circle bisects the circumference of the other means that the common chord of the two circles is a diameter of one of them. The equation of the common chord is obtained by subtracting the equations of the two circles: (x2+y2−2r1x−2r1y+r12)−(x2+y2−2r2x−2r2y+r22)=0 2(r2−r1)x+2(r2−r1)y+(r12−r22)=0 Assuming r1=r2, we divide by r2−r1: 2x+2y−(r1+r2)=0
If the common chord is a diameter of the circle with radius r2, its center (r2,r2) must lie on the common chord: 2r2+2r2−(r1+r2)=0 4r2−r1−r2=0 3r2=r1
This implies that one radius is three times the other. Let the radii be r and 3r. Thus, {r1,r2}={r,3r}. Using Vieta's formulas: Sum of radii: r1+r2=r+3r=4r. From Vieta's formulas, r1+r2=2(a+b). So, 4r=2(a+b)⟹2r=a+b. Product of radii: r1r2=r⋅3r=3r2. From Vieta's formulas, r1r2=a2+b2. So, 3r2=a2+b2.
Substitute r=2a+b into the product equation: 3(2a+b)2=a2+b2 34(a+b)2=a2+b2 3(a2+2ab+b2)=4(a2+b2) 3a2+6ab+3b2=4a2+4b2 a2−6ab+b2=0
