Question

4^{5log_{4\sqrt{2}}(3-\sqrt{6})-6log_{8}(\sqrt{3}-\sqrt{2})}

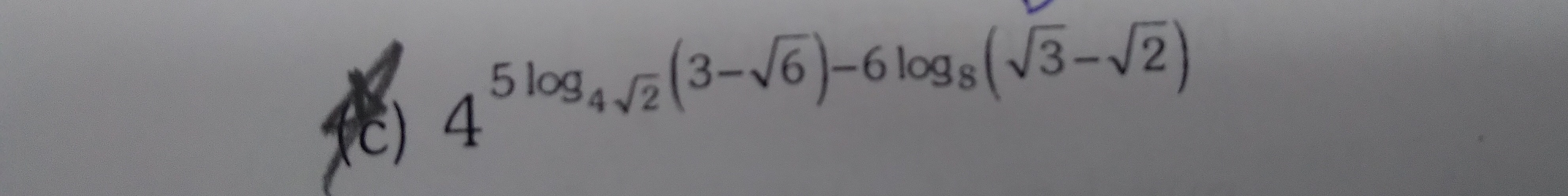
Answer 1

9

Answer 2

1. Convert logarithm bases to 2: $4\sqrt{2} = 2^{5/2}$ and $8 = 2^3$.
2. Simplify exponent terms: $5log_{4\sqrt{2}}(3-\sqrt{6}) = 5 \cdot \frac{1}{5/2} log_2(3-\sqrt{6}) = 2 log_2(3-\sqrt{6})$. $6log_{8}(\sqrt{3}-\sqrt{2}) = 6 \cdot \frac{1}{3} log_2(\sqrt{3}-\sqrt{2}) = 2 log_2(\sqrt{3}-\sqrt{2})$.
3. Combine terms: $2 log_2(3-\sqrt{6}) - 2 log_2(\sqrt{3}-\sqrt{2}) = 2 log_2\left(\frac{3-\sqrt{6}}{\sqrt{3}-\sqrt{2}}\right)$.
4. Simplify the argument: $\frac{3-\sqrt{6}}{\sqrt{3}-\sqrt{2}} = \frac{\sqrt{3}(\sqrt{3}-\sqrt{2})}{\sqrt{3}-\sqrt{2}} = \sqrt{3}$.
5. The exponent becomes $2 log_2(\sqrt{3}) = log_2((\sqrt{3})^2) = log_2(3)$.
6. Evaluate the expression: $4^{log_2(3)} = (2^2)^{log_2(3)} = 2^{2 \cdot log_2(3)} = 2^{log_2(3^2)} = 2^{log_2(9)} = 9$.