Question

If g(x) = [f(2f(x) + 2)]² and f(0) = -1. f'(0) = 1, then g'(0) is

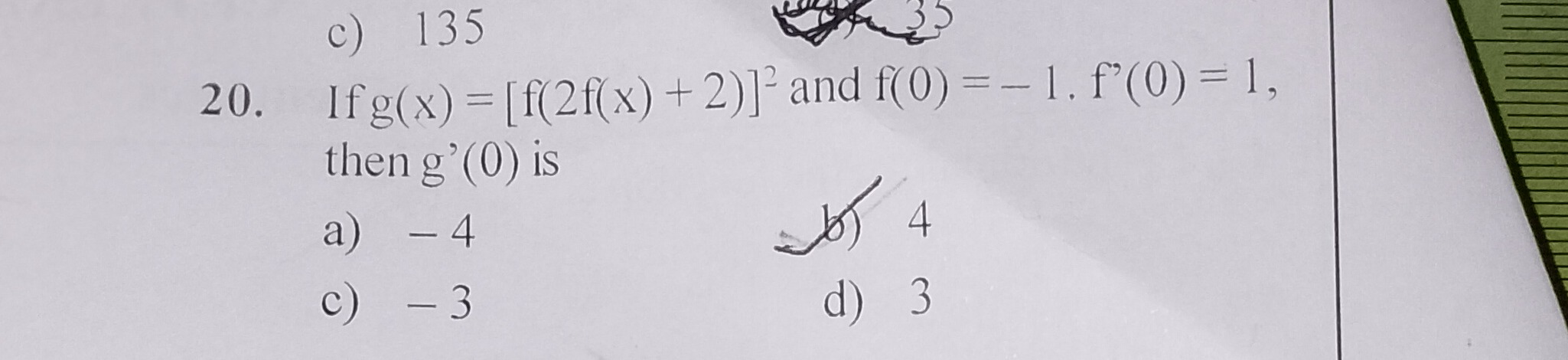
• A. -4
• B. 4
• C. -3
• D. 3

Answer 1

Answer: (A)

-4

Answer 2

Given:

$$g(x) = \left[ f\Big(2f(x)+2\Big) \right]^2$$

Differentiate using the chain rule:

$$g'(x) = 2f(2f(x)+2) \cdot f'(2f(x)+2) \cdot \frac{d}{dx}(2f(x)+2)$$

Since $\frac{d}{dx}(2f(x)+2) = 2f'(x)$, we have:

$$g'(x) = 4\, f(2f(x)+2) \, f'(2f(x)+2) \, f'(x)$$

At $x = 0$:

• $f(0) = -1$
• $f'(0) = 1$
• Compute $2f(0)+2 = 2(-1)+2 = 0$ Thus,
• $f(2f(0)+2) = f(0) = -1$
• $f'(2f(0)+2) = f'(0) = 1$

Substitute these values:

$$g'(0) = 4 \times (-1) \times 1 \times 1 = -4$$