Question

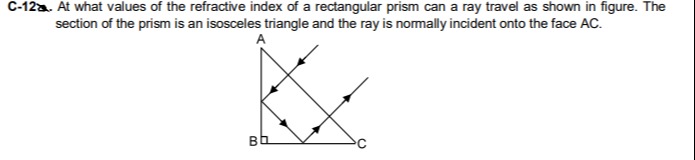
At what values of the refractive index of a rectangular prism can a ray travel as shown in figure. The section of the prism is an isosceles triangle and the ray is normally incident onto the face AC.

Answer 1

μ ≥ √2

Answer 2

1. Identify the type of prism: The problem states it's an isosceles triangle and shows a right angle at B. Thus, it's a right-angled isosceles prism with angles $90^\circ, 45^\circ, 45^\circ$.

2. Analyze the ray path: The ray undergoes two total internal reflections (TIR) inside the prism. For TIR to occur, the angle of incidence ($i$) at the internal surface must be greater than or equal to the critical angle ($C$).

3. Determine the critical angle: The critical angle $C$ is related to the refractive index $\mu$ by the formula $\sin C = \frac{1}{\mu}$ (assuming the outside medium is air, $\mu_{air}=1$).

4. Determine the angles of incidence for TIR: In a right-angled isosceles prism, when light undergoes TIR, the angle of incidence is typically $45^\circ$ (e.g., if a ray enters normally on one of the shorter faces and hits the hypotenuse, or vice versa, or if the ray is parallel to one of the sides). For the ray to travel as shown, undergoing two reflections, the angles of incidence for these internal reflections must be $45^\circ$.

5. Apply the condition for TIR: For TIR to occur, $i \ge C$. Substituting $i=45^\circ$: $45^\circ \ge C$

   Taking the sine of both sides (since $\sin x$ is increasing for $x \in [0, 90^\circ]$): $\sin 45^\circ \ge \sin C$ $\frac{1}{\sqrt{2}} \ge \frac{1}{\mu}$

   Rearranging the inequality: $\mu \ge \sqrt{2}$

Thus, the refractive index of the prism must be greater than or equal to $\sqrt{2}$ for the ray to travel as shown.

The final answer is $\mu \ge \sqrt{2}$.