Question

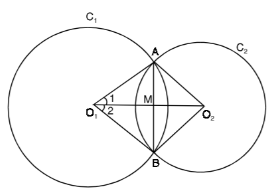
${{C}_{1}}$and ${{C}_{2}}$ are two circles with center ${{O}_{1}}$ and ${{O}_{2}}$ and intersect each other at points $A$ and $B$. If ${{O}_{1}}{{O}_{2}}$ intersect $AB$ at $M$ then show that $M$ is the midpoint of $AB$.

Answer 1

Hint: We will try to show \Delta {{O}_{1}}AB$$$$\cong $$$$\Delta {{O}_{2}}AB using ‘SSS’ type of triangle congruency and then we will show $\Delta {{O}_{1}}AM\cong \Delta {{O}_{1}}BM$ using ‘SAS’ type of triangle congruency and finally we will show $M$ is the midpoint of $AB$.

Given that two circles ${{C}_{1}}$and ${{C}_{2}}$ with the center ${{O}_{1}}$ and ${{O}_{2}}$ intersect each other at points $A$ and $B$.
Also, ${{O}_{1}}{{O}_{2}}$ intersects $AB$ at $M$.
Then, we have to show that $M$ is the midpoint of $AB$.

Let us assume that the radius of the circle ${{C}_{1}}$ be $r$ and the radius of the circle ${{C}_{2}}$ be $s$.
Proof:
In $\Delta {{O}_{1}}A{{O}_{2}}$ and $\Delta {{O}_{1}}B{{O}_{2}}$, we have
${{O}_{1}}A={{O}_{1}}B.....\left( i \right)$
Both are radii of the same circle ${{C}_{1}}$.
$\Rightarrow {{O}_{2}}A={{O}_{2}}B.....\left( ii \right)$
Both are radii of the same circle ${{C}_{2}}$.
Also, ${{O}_{1}}{{O}_{2}}={{O}_{2}}{{O}_{1}}....\left( iii \right)$
Common sides of both the triangles $\Delta {{O}_{1}}A{{O}_{2}}$and $\Delta {{O}_{1}}B{{O}_{2}}$
So, from the equation $\left( i \right),\left( ii \right)$and$\left( iii \right)$, we get both triangles $\Delta {{O}_{1}}A{{O}_{2}}$ and $\Delta {{O}_{1}}B{{O}_{2}}$ are congruent with each other by ‘SSS’ type of triangle congruency.
Or, $\Delta {{O}_{1}}A{{O}_{2}}\cong \Delta {{O}_{1}}B{{O}_{2}}$ by SSS type of triangle congruency.
(Here, ‘SSS’ type means side – side – side type of triangle congruency)
SSS – Theorem

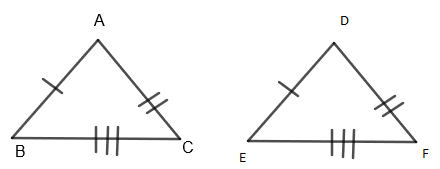
Side-side - side postulate (SSS) states that two triangles are congruent if three sides of one triangle are congruent to the corresponding sides of the other triangle.
Here, from $\Delta ABC$ and $\Delta DEF$, we can say that
$AB=DF....\left( a \right)$
$AC=DE....\left( b \right)$
$BC=EF....\left( c \right)$
So, from the equation $\left( a \right),\left( b \right)$ and $\left( c \right)$, we have $\Delta ABC\cong \Delta DEF$ by SSS – type triangle congruency which clearly shows that
$\Rightarrow M\angle {{O}_{2}}{{O}_{1}}A=M\angle {{O}_{2}}{{O}_{1}}B....\left( iv \right)$ by CPCT
(Here, CPCT is corresponding parts of the congruent triangle)
Also, we have,
$\Rightarrow M\angle M{{O}_{1}}A=M\angle M{{O}_{1}}B....\left( v \right)$
From the equation $\left( iv \right)$, both are the same angle.
$\Rightarrow {{O}_{1}}A={{O}_{1}}B.....\left( vi \right)$ by CPCT
Now, in $\Delta AM{{O}_{1}}$and $\Delta BM{{O}_{1}}$, we have
$\Rightarrow {{O}_{1}}A={{O}_{1}}B....\left( vii \right)$
(Both are radii of the same circle)
$\Rightarrow m\angle M{{O}_{1}}A=M\angle M{{O}_{1}}B.....\left( viii \right)$
From corresponding parts of the congruent triangle.
$\Rightarrow {{O}_{1}}M=M{{O}_{1}}.....\left( ix \right)$
The common side of both the triangles $\Delta AM{{O}_{1}}$and $\Delta BM{{O}_{1}}$.
So, from the equation $\left( vii \right),\left( viii \right)$and $\left( ix \right)$, we get both triangles $\Delta AM{{O}_{1}}$and $\Delta BM{{O}_{1}}$ are congruent with each other by the SAS test of triangle congruency.
Or, $\Delta AM{{O}_{1}}\cong BM{{O}_{1}}$ by ’SAS’ test of triangle congruency.
(Here, ‘SAS’ means Side – Angle – Side type of triangle congruency)
SAS – theorem

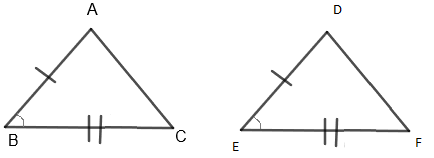
If any two sides and the angle included between one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
Here in the diagram,
Side $AB=DE$
Also side $BC=EF$
And $\angle ABC=\angle DEF$
Thus, $\Delta ABC\cong \Delta DEF$ by SAS type of triangle congruency.
Also, from this, we have$AM=BM$ by the corresponding part of congruent triangles $\Delta AM{{O}_{1}}\cong \Delta BM{{O}_{{}}}$ which means that $M$ is the midpoint of $AB$.
Hence proved.
Note: Visualize the geometry first before attempting the question. Make a clear diagram of the required question which reduces the probability of error in your solution using the SSS and SAS theorems to prove triangles are congruent, we prove the required statement.