Question

By pulling the cord of a yo-yo just fast enough, a person manages to make the yo-yo spin counter-clockwise, while remaining at a constant height above the floor. Denoting the weight of the yo-yo by $W$ . The radius of the inner drum on which the cord is wound by $r$ , and the radius of gyration of the yo-yo by $k$ , determine;
(A) The tension in the cord
(B) The angular acceleration of the yo-yo

Answer 1

Hint In this question, we need to determine the direction of the acceleration of the yo-yo. Newton’s laws of motion and the relation between the moment of inertia, torque, and the acceleration of the body are used to solve the question

Complete Step-by-step solution

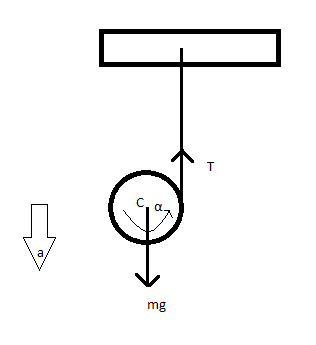
When the yo-yo is released from the hand, then the hand works as rigid support and the wrapped string starts unwrapping so that the yo-yo gains some instant. The linear acceleration $a$ in a vertically downward direction. Angular acceleration $\alpha$ about its center. The force $mg$ works vertically downward. The tension $T$ in an upward direction.
From FBD applying force equation,
$mg - T = ma$ ................... $\left( 1 \right)$
Applying torque equation about the center $C$, $\tau = I\alpha$
$\Rightarrow T \times r + mg\left( 0 \right) = I\alpha$
$\Rightarrow Tr = I\alpha$
$\Rightarrow T = \dfrac{{I\alpha }}{r}$..................... $\left( 2 \right)$
Moment of Inertia for yo-yo is:
$\Rightarrow I = \dfrac{1}{2}m{r^2}$
On putting the value of $I$in the equation$\left( 2 \right)$;
$\Rightarrow T = \dfrac{1}{2}m{r^2} \times \left( {\dfrac{\alpha }{r}} \right)$
$\Rightarrow T = \dfrac{1}{2}m \times r\alpha$
$\therefore T = \dfrac{1}{2}ma$ $\left[ {\because a = r\alpha } \right]$............... $\left( 3 \right)$
On putting the value $T$ into the equation $\left( 1 \right)$ ;
$\Rightarrow mg - \dfrac{1}{2}ma = ma$
$\therefore mg = ma + \dfrac{1}{2}ma$
Taking $m$ common out and get canceled;
$\Rightarrow g = \dfrac{3}{2}a$
$\therefore a = \dfrac{2}{3}g$..............................$\left( 4 \right)$
As we know, the formula for angular acceleration is;
$\therefore \alpha = \dfrac{a}{r}$
Substituting the value of $a$ from the equation$\left( 4 \right)$;
$\Rightarrow \alpha = \dfrac{{2g}}{{3r}}$
Hence, the Tension in the cord is $\dfrac{1}{2}ma$ and the angular acceleration of the yo-yo is $\left( {\dfrac{{2g}}{{3r}}} \right)$ .

Additional Information The torque of all the forces is zero, which passes through the point at which the torque has been computed. When a force is applied to the body, not only the applied force is acting, there are many other forces like gravitational force f and the normal force N that balances the other force. Therefore in the force equation
$\Rightarrow \overrightarrow {{F_{net}}} =$ $m\overrightarrow a$,
$\therefore {\overrightarrow F _{net}} = {\overrightarrow F _{ex}} + \overrightarrow F g + \overrightarrow f + \overrightarrow N$

Note Students should keep in mind that the weight of an object is the gravitational force applied in a downward direction. Students also need to know that the unbalanced force is the cause of motion. So that they can easily compare the forces exerted on a mechanical system and determine the direction of motion.