Question
Question: By applying a force \(F = \left( {3xy - 5z} \right)\mathop j\limits^ \wedge + 4z\mathop k\limits^ \w...
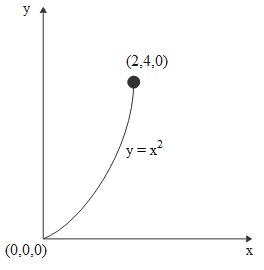
By applying a force F=(3xy−5z)j∧+4zk∧ a particle is moved along the path y=x2 from point (0,0,0) to the point (2,4,0). The work done by the F on the particle is (all values are in SI units)
A. 5280J
B. 5140J
C. 5232J
D. 5192J
Solution
Work done on a particle by force is the dot product of the force and the displacement. Hence work done is not a vector and it is a scalar quantity. If force and displacement are perpendicular to each other then the work done will be zero as dot product between them will become zero. In this problem we apply the same concept to find the work done.
Formula used:
(x1,y1,z1)∫(x2,y2,z2)F→.ds→=W
Complete answer:
To denote the position of a point on a coordinate system from the origin we denote it by using a vector notation. If x-coordinate is x and y-coordinate is y then the vector notation to denote that point is xi∧+yj∧. Now the unit vector of this vector gives us the direction of this vector. The property of unit vector is even if we multiply the unit vector with any magnitude the direction will remain the same but only magnitude changes.
We have force vector as F=(3xy−5z)j∧+4zk∧
Path of the particle is y=x2. This clearly tells us the particle is moving in the x-y plane while the force is having k∧ component which means force component in z- direction. The angle between this z- component of force and displacement of the particle is ninety degrees. So this component won't contribute to any work.
The remaining force term is (3xy−5z)j∧. But our trajectory doesn’t have the z- coordinate at all hence we can remove that ‘5z’ term too. So the effective force will become F=(3xy)j∧
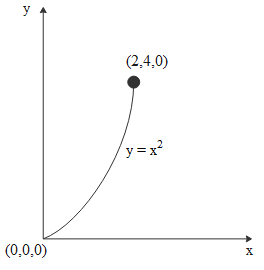
The trajectory is
y=x2
⇒x=y
So by substituting x=y in F=(3xy)j∧ we get the force expression as
F=(3xy)j∧
\eqalign{
& \Rightarrow F = \left( {3(\sqrt y )y} \right)\mathop j\limits^ \wedge \cr
& \Rightarrow F = \left( {3{y^{\dfrac{3}{2}}}} \right)\mathop j\limits^ \wedge \cr}
Now the work done will be
(x1,y1,z1)∫(x2,y2,z2)F→.ds→=W
\eqalign{
& \Rightarrow \int\limits_{(0,0,0)}^{(2,4,0)} {\left( {3{y^{\dfrac{3}{2}}}} \right)\mathop j\limits^ \wedge } .\left( {\mathop {dy}\limits^ \to } \right)\mathop j\limits^ \wedge = W \cr
& \Rightarrow \dfrac{{3{y^{(1 + \dfrac{3}{2})}}}}{{1 + \dfrac{3}{2}}} = W \cr
& \Rightarrow \dfrac{6}{5}{y^{\dfrac{5}{2}}} = W \cr
& \Rightarrow \dfrac{6}{5}\left[ {{4^{\dfrac{5}{2}}} - {0^{\dfrac{5}{2}}}} \right] = W \cr
& \Rightarrow W = \dfrac{6}{5} \times 32 = \dfrac{{192}}{5}J \cr}
So, the correct answer is “Option D”.
Note:
The particle is moving in the x-y plane and z axis will be normal to the x-y plane, Hence the work done by any amount of force which acts along the z axis will be zero. Similarly work done by centripetal force in circular motion is zero as displacement and force vectors will be perpendicular.
