Question

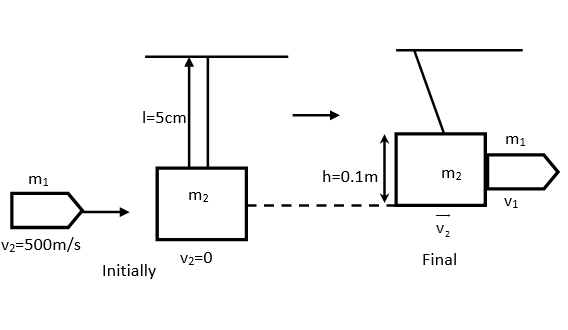
Bullet of mass $0.01kg$ and travelling at a speed of $500m/s$ strikes and passes horizontally through a block of mass $2kg$ which is suspended by a string of length$5m$. The centre of gravity of the block is found to raise a vertical distance of$0.1m$. What is the speed of the bullet after it emerges from the block $(g = 9.8m/{s^2})(time$of the passing of bullets is negligible)

Answer 1

Concept of conservation of energy and conservation of momentum as in such collisions total energy and momentum always remains conserved.

Formula used:
1. Kinetic energy $=$Potential energy.
2. Initial momentum $=$Final momentum

Complete step by step answer:
Let ${m_1}\,\,and\,\,{m_2}$ be the masses of bullet and block respectively.
${u_1} =$initial velocity of bullet
${u_1} = 500m/s$
${u_2} =$initial velocity of block $= 0m/s$
${v_1} =$final velocity of block
${v_2} =$final velocity of block
Since, the block raises to a height $h = 0.1m$after collision, so its kinetic energy is converted into potential energy i.e.
$K.E = P.E$
$\dfrac{1}{2}{m_2}{v_2}^2 = {m_2}gh$
Where $g$is acceleration due to gravity $= 9.8m/{s^2}$
So,
$\dfrac{1}{2}v_2^2 = gh$
$\Rightarrow v_2^2 = 2gh \\\ \Rightarrow v_2^{} = \sqrt {2gh} \\\$
Putting $g = 9.8m/s$and $h = 0.1m$we, have
${v_2} = \sqrt {2 \times 9.8 \times 0.1} \\\ {v_2} = 1.4m/s \\\$

Now, by conservation of momentum, we have
Initial momentum $=$final momentum
$\Rightarrow {m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}$
$\Rightarrow {m_1}{u_1} + {m_2}(0) = {m_1}{v_1} + {m_2}{v_2}$
$\Rightarrow {m_1}{u_1} = {m_1}{v_1} + {m_2}{v_2}$
$\Rightarrow {m_1}{v_1} = {m_1}{u_1} - {m_2}{v_2}$
$\Rightarrow {v_1} = \dfrac{{{m_1}{u_1} - {m_2}{v_2}}}{{{m_1}}}$
Here,
${m_1} =$mass of bullet $= 0.01kg$
${m_2} =$mass of block $= 2kg$
${u_1} = 500m/s,\,\,{v_2} = 1.4m/s$
On substituting these values, we get
So,
${v_1} = \dfrac{{(0.01 \times 500) - (2 \times 1.4)}}{{0.01}}m/s$
${v_1} = \dfrac{{5 - 2.8}}{{0.01}}m/s$
Hence, ${v_1} = \dfrac{{2.2}}{{0.01}}m/s$
${v_1} = 220m/s$
The bullet will emerge out with a speed of $220m/s$from the block

Note:
Remember as after hitting with the bullet, the block attains some height from the initial reference level. That is why we used the concept $K.E = P.E$ and found the velocity of the block from here.