Question

q) $y = \sqrt{\log_2 3 \cdot \log_2 12 + \log_2 48 \log_2 192 + 16 - \log_2 \frac{1}{2} \log_2 48}$

Answer 1

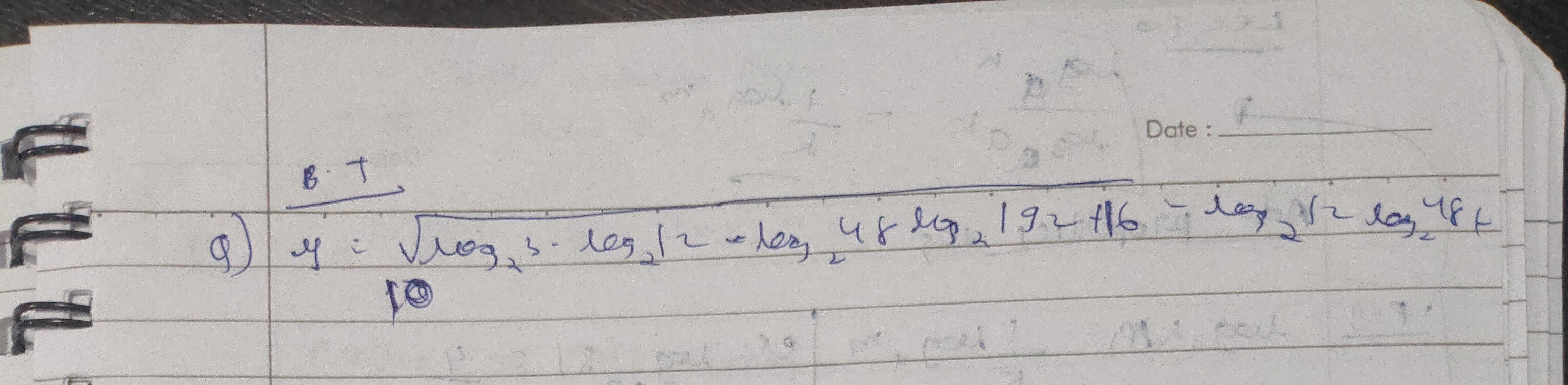
$\sqrt{2(\log_2 3)^2 + 13\log_2 3 + 44}$

Answer 2

To simplify the given expression for $y$, we will first express all logarithms in terms of a common base and a common variable. Let $a = \log_2 3$.

The terms inside the square root involve logarithms of 3, 12, 48, 192, and $\frac{1}{2}$. Let's express each of these in terms of $a$:

1. $\log_2 3 = a$
2. $\log_2 12 = \log_2 (3 \cdot 4) = \log_2 (3 \cdot 2^2) = \log_2 3 + \log_2 2^2 = a + 2$
3. $\log_2 48 = \log_2 (3 \cdot 16) = \log_2 (3 \cdot 2^4) = \log_2 3 + \log_2 2^4 = a + 4$
4. $\log_2 192 = \log_2 (3 \cdot 64) = \log_2 (3 \cdot 2^6) = \log_2 3 + \log_2 2^6 = a + 6$
5. $\log_2 \frac{1}{2} = \log_2 2^{-1} = -1$

Now, substitute these expressions back into the equation for $y$: $y = \sqrt{\log_2 3 \cdot \log_2 12 + \log_2 48 \log_2 192 + 16 - \log_2 \frac{1}{2} \log_2 48}$ $y = \sqrt{a(a+2) + (a+4)(a+6) + 16 - (-1)(a+4)}$

Expand each product: $a(a+2) = a^2 + 2a$ $(a+4)(a+6) = a^2 + 6a + 4a + 24 = a^2 + 10a + 24$ $-(-1)(a+4) = 1(a+4) = a+4$

Substitute these expanded forms back into the expression for $y$: $y = \sqrt{(a^2 + 2a) + (a^2 + 10a + 24) + 16 + (a+4)}$

Combine like terms inside the square root: $y = \sqrt{ (a^2 + a^2) + (2a + 10a + a) + (24 + 16 + 4) }$ $y = \sqrt{ 2a^2 + 13a + 44 }$

The expression inside the square root is a quadratic in $a$. This quadratic does not appear to be a perfect square of an integer or a simple rational expression. The discriminant $D = b^2 - 4ac = 13^2 - 4(2)(44) = 169 - 352 = -183$, which is negative. This means the quadratic has no real roots and thus cannot be factored into linear terms with real coefficients.

Therefore, the simplified form of $y$ is: $y = \sqrt{2(\log_2 3)^2 + 13(\log_2 3) + 44}$

The question asks to solve for $y$, which means to simplify the expression. The expression is simplified to its most compact form.