Question

Two circular loops A and B are made of the same wire and their radii are in the ratio 1 : n. Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio 1 : m. The relation between m and n is

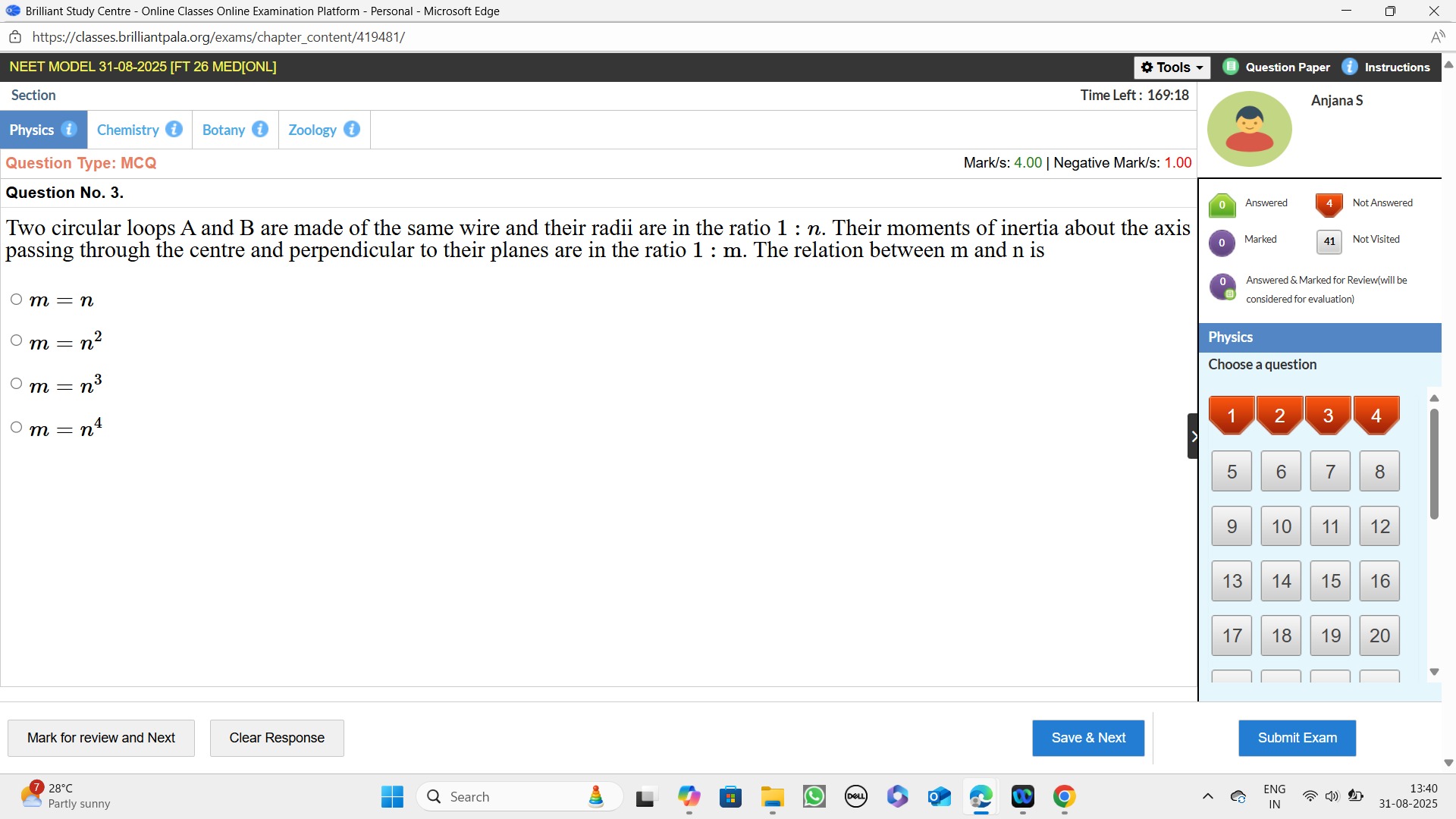
• A. m = n
• B. m = $n^2$
• C. m = $n^3$
• D. m = $n^4$

Answer 1

Answer: (C)

m = $n^3$

Answer 2

The moment of inertia of a circular loop of mass $M$ and radius $R$ about an axis passing through its center and perpendicular to its plane is given by $I = MR^2$. The mass of the loop is related to its linear mass density $\lambda$ and its circumference $2\pi R$ by $M = \lambda (2\pi R)$. Therefore, the moment of inertia becomes $I = (\lambda 2\pi R) R^2 = 2\pi \lambda R^3$.

Since both loops A and B are made of the same wire, they have the same linear mass density, $\lambda$. Let $R_A$ and $R_B$ be the radii of loops A and B, and $I_A$ and $I_B$ be their respective moments of inertia. We are given the ratio of radii: $\frac{R_A}{R_B} = \frac{1}{n}$. We are given the ratio of moments of inertia: $\frac{I_A}{I_B} = \frac{1}{m}$.

Using the formula $I = 2\pi \lambda R^3$, we can write the ratio of moments of inertia: $\frac{I_A}{I_B} = \frac{2\pi \lambda R_A^3}{2\pi \lambda R_B^3} = \left(\frac{R_A}{R_B}\right)^3$ Substituting the given ratios: $\frac{1}{m} = \left(\frac{1}{n}\right)^3 = \frac{1}{n^3}$ Thus, the relation between $m$ and $n$ is $m = n^3$.