Question
Question: A satellite of mass *m* is revolving in a circular orbit of radius 2*R*, around the earth of mass *M...
A satellite of mass m is revolving in a circular orbit of radius 2R, around the earth of mass M. The work done to shift the satellite to an orbit of radius 3R is
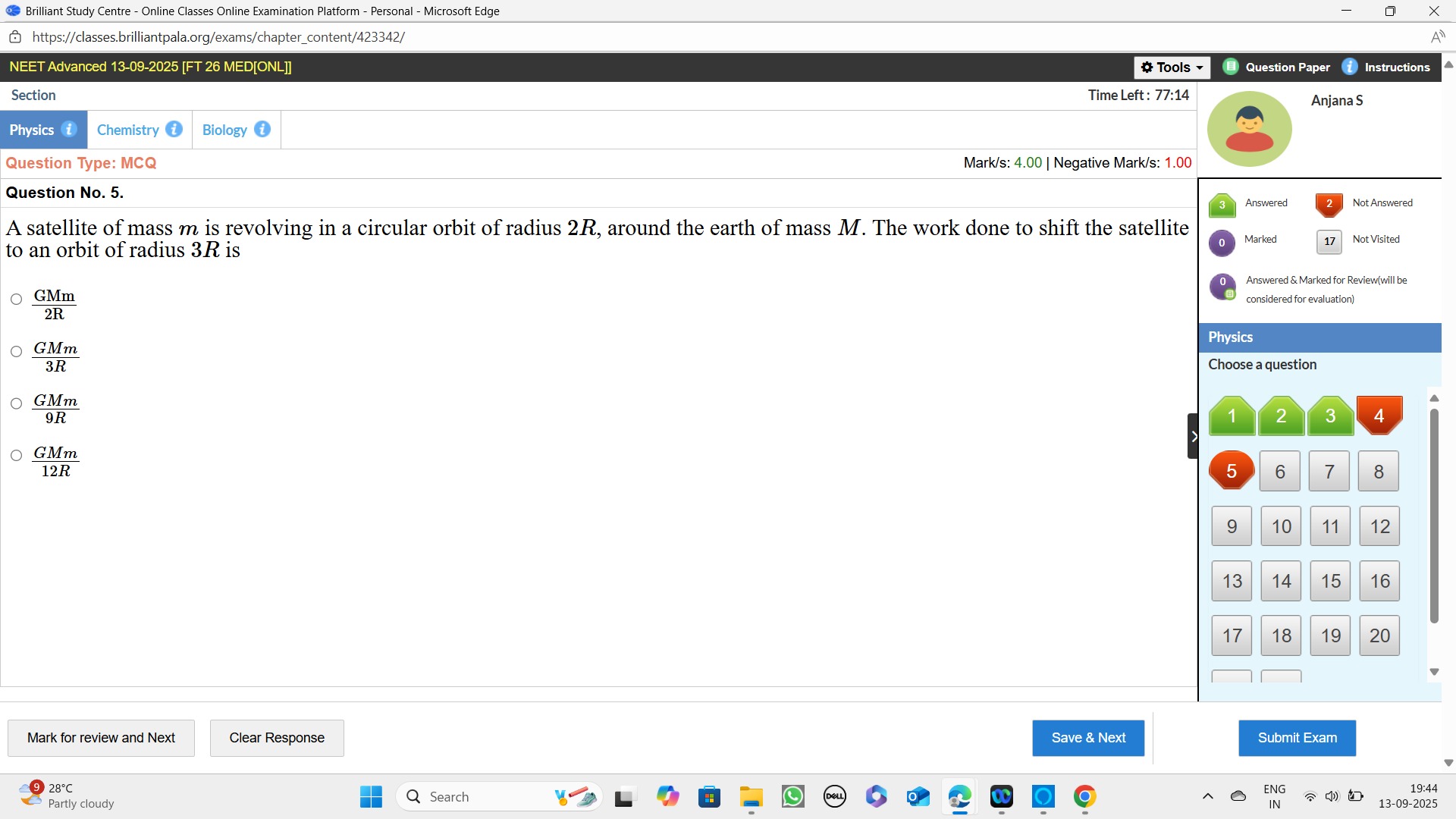
2RGMm
3RGMm
9RGMm
12RGMm
12RGMm
Solution
The total mechanical energy of a satellite of mass m in a circular orbit of radius r around a planet of mass M is given by E=−2rGMm. The work done to shift the satellite from an initial orbit of radius r1 to a final orbit of radius r2 is the difference in their total energies: W=E2−E1.
Given: Initial orbit radius, r1=2R Final orbit radius, r2=3R
Initial energy, E1=−2r1GMm=−2(2R)GMm=−4RGMm Final energy, E2=−2r2GMm=−2(3R)GMm=−6RGMm
Work done, W=E2−E1=(−6RGMm)−(−4RGMm) W=−6RGMm+4RGMm To combine these terms, we find a common denominator, which is 12R: W=−12R2GMm+12R3GMm W=12RGMm
