Solveeit Logo
Login

Question

Question: $2.68 \times 10^{-3}$ mol $A^{n+}$ (aq) require $1.61 \times 10^{-3}$ mol $MnO_4^-$ (aq) for oxidati...

2.68×10−32.68 \times 10^{-3} mol An+A^{n+} (aq) require 1.61×10−31.61 \times 10^{-3} mol MnO4−MnO_4^- (aq) for oxidation of An+A^{n+} (aq) to AO3−AO_3^- (aq) in acidic medium. The value of 'n' is

A

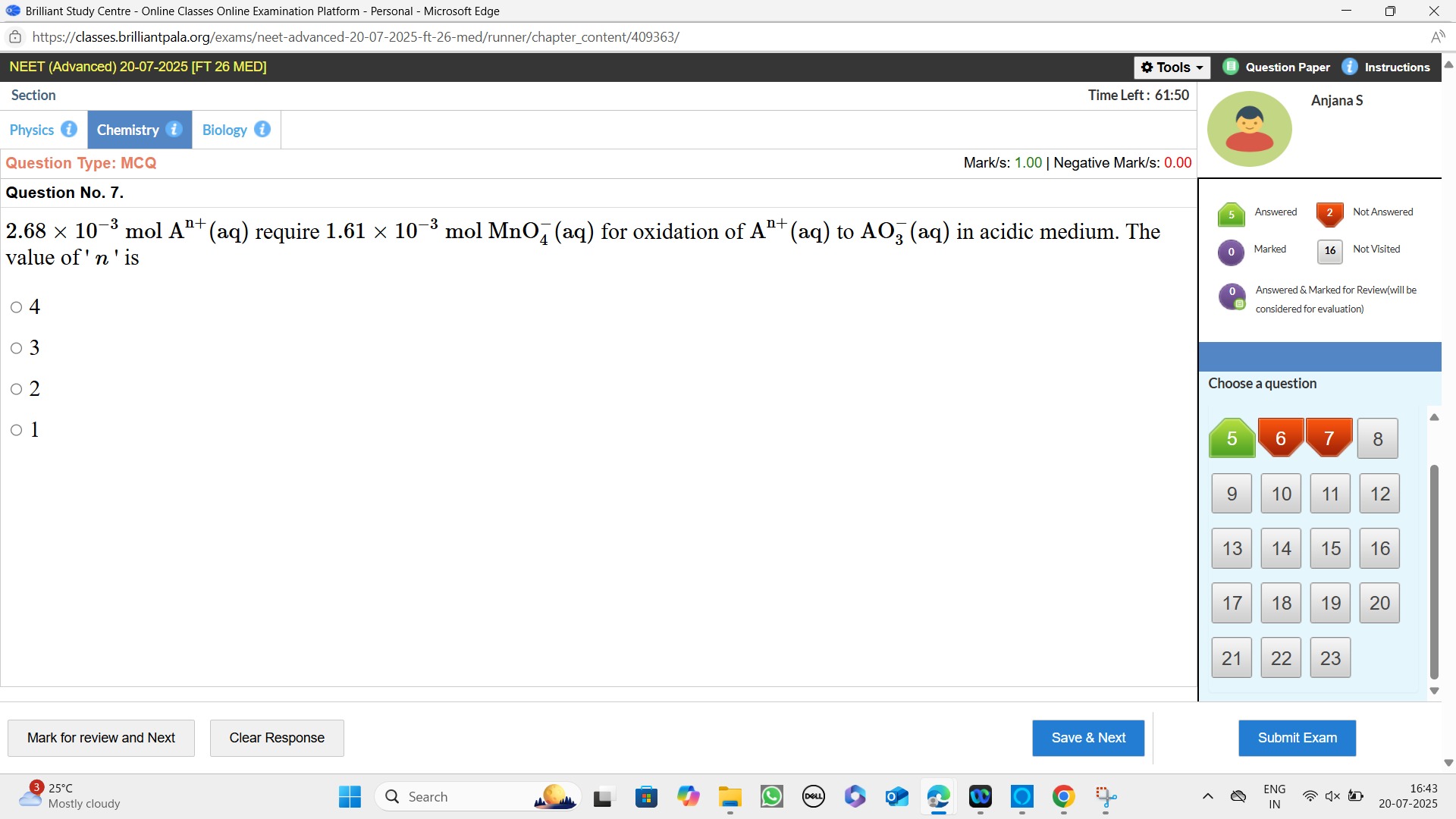
4

B

3

C

2

D

1

Answer

2

Explanation

Solution

To determine the value of 'n', we need to consider the electron exchange in the redox reaction.

  1. Identify the oxidation and reduction half-reactions:

    • Oxidation of An+A^{n+} to AO3−AO_3^-:
      The oxidation state of A in An+A^{n+} is +n.
      The oxidation state of A in AO3−AO_3^- is calculated as:
      A+3(−2)=−1A + 3(-2) = -1
      A−6=−1A - 6 = -1
      A=+5A = +5
      So, A is oxidized from +n to +5. The number of electrons lost per mole of An+A^{n+} is (5 - n).
      The balanced oxidation half-reaction is:
      An++3H2O→AO3−+6H++(5−n)e−A^{n+} + 3H_2O \rightarrow AO_3^- + 6H^+ + (5-n)e^-

    • Reduction of MnO4−MnO_4^- in acidic medium:
      In acidic medium, MnO4−MnO_4^- (Manganese in +7 oxidation state) is reduced to Mn2+Mn^{2+} (Manganese in +2 oxidation state).
      The number of electrons gained per mole of MnO4−MnO_4^- is (7 - 2) = 5.
      The balanced reduction half-reaction is:
      MnO4−+8H++5e−→Mn2++4H2OMnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O

  2. Apply the concept of electron equivalence:
    In any redox reaction, the total number of electrons lost by the reducing agent must be equal to the total number of electrons gained by the oxidizing agent.

    Moles of electrons lost by An+A^{n+} = (Moles of An+A^{n+}) × (electrons lost per mole of An+A^{n+})
    Moles of electrons gained by MnO4−MnO_4^- = (Moles of MnO4−MnO_4^-) × (electrons gained per mole of MnO4−MnO_4^-)

    Given:
    Moles of An+A^{n+} = 2.68×10−32.68 \times 10^{-3} mol
    Moles of MnO4−MnO_4^- = 1.61×10−31.61 \times 10^{-3} mol

    Equating the moles of electrons exchanged:
    (2.68×10−3)×(5−n)=(1.61×10−3)×5(2.68 \times 10^{-3}) \times (5 - n) = (1.61 \times 10^{-3}) \times 5

  3. Solve for 'n':
    Divide both sides by 10−310^{-3}:
    2.68×(5−n)=1.61×52.68 \times (5 - n) = 1.61 \times 5
    2.68×(5−n)=8.052.68 \times (5 - n) = 8.05

    5−n=8.052.685 - n = \frac{8.05}{2.68}
    5−n≈3.00375 - n \approx 3.0037

    Rounding to the nearest integer, we get:
    5−n=35 - n = 3
    n=5−3n = 5 - 3
    n=2n = 2

The value of 'n' is 2.