Question

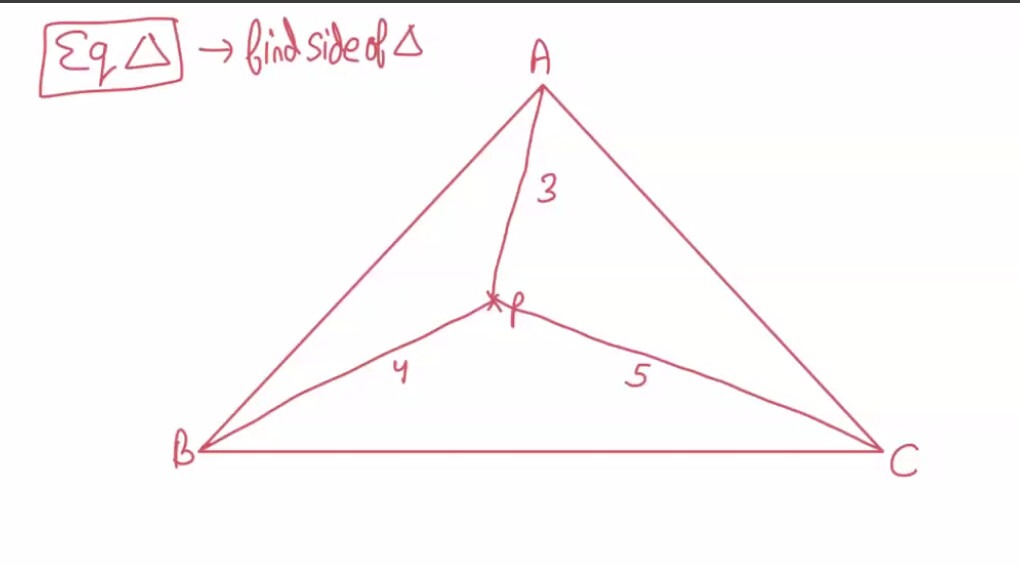
$\boxed{Eq \triangle}$ $\rightarrow$ find side of $\triangle$

Answer 1

$\sqrt{25 + 12\sqrt{3}}$

Answer 2

To find the side of the equilateral triangle ABC, given an internal point P with distances PA=3, PB=4, PC=5, we use a geometric transformation method (rotation).

1. Rotation: Rotate the triangle $\triangle APB$ about vertex A by $60^\circ$ counter-clockwise.

• Vertex A remains at A.
• Vertex B moves to vertex C (since $\triangle ABC$ is equilateral and the rotation is $60^\circ$ about A).
• Point P moves to a new point P'.

2. Properties of the Rotated Triangle:

• The rotated triangle is $\triangle AP'C$.
• Due to rotation, lengths are preserved: $AP' = AP = 3$ and $P'C = PB = 4$.
• Since P is rotated to P' about A by $60^\circ$, the triangle $\triangle APP'$ is equilateral. Therefore, $PP' = AP = 3$.

3. Analyzing Triangle $\triangle PP'C$: We now have a triangle $\triangle PP'C$ with side lengths:

• $PP' = 3$
• $P'C = 4$
• $PC = 5$ (given) Notice that $3^2 + 4^2 = 9 + 16 = 25 = 5^2$. This means $\triangle PP'C$ is a right-angled triangle, with the right angle at $P'$. So, $\angle PP'C = 90^\circ$.

4. Finding Angle $\angle AP'C$: The angle $\angle AP'C$ is composed of $\angle AP'P$ and $\angle PP'C$.

• Since $\triangle APP'$ is equilateral, $\angle AP'P = 60^\circ$.
• From step 3, $\angle PP'C = 90^\circ$. Since P is an internal point of $\triangle ABC$, P' will be positioned such that these angles add up. Therefore, $\angle AP'C = \angle AP'P + \angle PP'C = 60^\circ + 90^\circ = 150^\circ$.

5. Applying the Law of Cosines to $\triangle AP'C$: Let 'a' be the side length of the equilateral triangle ABC (so $AC = a$). In $\triangle AP'C$, we have:

• $AP' = 3$
• $P'C = 4$
• $\angle AP'C = 150^\circ$ Using the Law of Cosines: $AC^2 = AP'^2 + P'C^2 - 2(AP')(P'C)\cos(\angle AP'C)$ $a^2 = 3^2 + 4^2 - 2(3)(4)\cos(150^\circ)$ $a^2 = 9 + 16 - 24(-\frac{\sqrt{3}}{2})$ $a^2 = 25 + 12\sqrt{3}$

6. Final Result: The side length 'a' of the equilateral triangle is $\sqrt{25 + 12\sqrt{3}}$.