Question

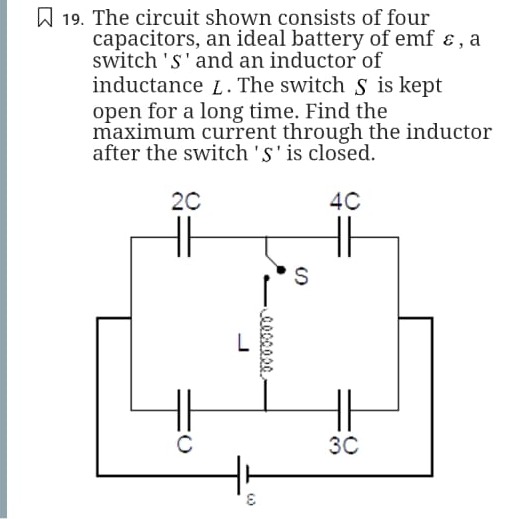
The circuit shown consists of four capacitors, an ideal battery of emf $\mathcal{E}$, a switch 'S' and an inductor of inductance $L$. The switch $S$ is kept open for a long time. Find the maximum current through the inductor after the switch 'S' is closed.

Answer 1

$I_{max}=\epsilon\,\sqrt{\frac{4C}{3L}}$

Answer 2

We first note that only the top‐branch capacitors (of capacitances 2C and 4C) are in the branch with the inductor. Since they are in series, their equivalent capacitance is

$$C_{top}=\frac{(2C)(4C)}{2C+4C}=\frac{8C^2}{6C}=\frac{4C}{3}\,.$$

For a long time before closing the switch, the top‐branch capacitors are uncharged while the bottom branch (with capacitors C and 3C in series) is charged by the battery. After closing the switch the circuit becomes a “forced LC” system. In the top branch the loop equation (taking the battery emf $\epsilon$ into account) is

$$\epsilon - v_C - v_L=0\,,$$

where the voltage across the capacitor network is

$$v_C=\frac{q}{C_{top}}$$

and the inductor voltage is $v_L=L\,\frac{d^2q}{dt^2}$ (with $i=\frac{dq}{dt}$). Thus we have

$$L\frac{d^2q}{dt^2}+\frac{q}{C_{top}}=\epsilon\,.$$

This is the equation of a harmonic oscillator with a forcing term and equilibrium charge $q_0=C_{top}\epsilon$. With the initial conditions (at $t=0$ the charge $q(0)=0$ and current $i(0)=0$), one finds that

$$q(t)=C_{top}\epsilon\Bigl(1-\cos(\omega t)\Bigr)$$

with

$$\omega=\frac{1}{\sqrt{L\,C_{top}}}\,.$$

Thus, the current in the inductor is

$$i(t)=\frac{dq}{dt}=C_{top}\epsilon\,\omega\sin(\omega t)\,.$$

Its maximum value occurs when $\sin(\omega t)=1$, hence

$$I_{max}=C_{top}\epsilon\,\omega=\epsilon\,C_{top}\,\frac{1}{\sqrt{L\,C_{top}}}=\epsilon\,\sqrt{\frac{C_{top}}{L}}\,.$$

Substitute $C_{top}=\frac{4C}{3}$ to obtain

$$I_{max}=\epsilon\,\sqrt{\frac{4C}{3L}}\,.$$

Summary:

1. Find the equivalent capacitance of the top branch: $C_{top}=\frac{4C}{3}$.
2. Write the LC loop equation using $q/C_{top}$ as the capacitor voltage and $L(d^2q/dt^2)$ for the inductor.
3. Solve the forced harmonic oscillator with equilibrium charge $q_0=C_{top}\epsilon$.
4. The current amplitude is $I_{max}=C_{top}\epsilon\,\omega=\epsilon\sqrt{C_{top}/L}$ and substituting $C_{top}$ gives the answer.