Question

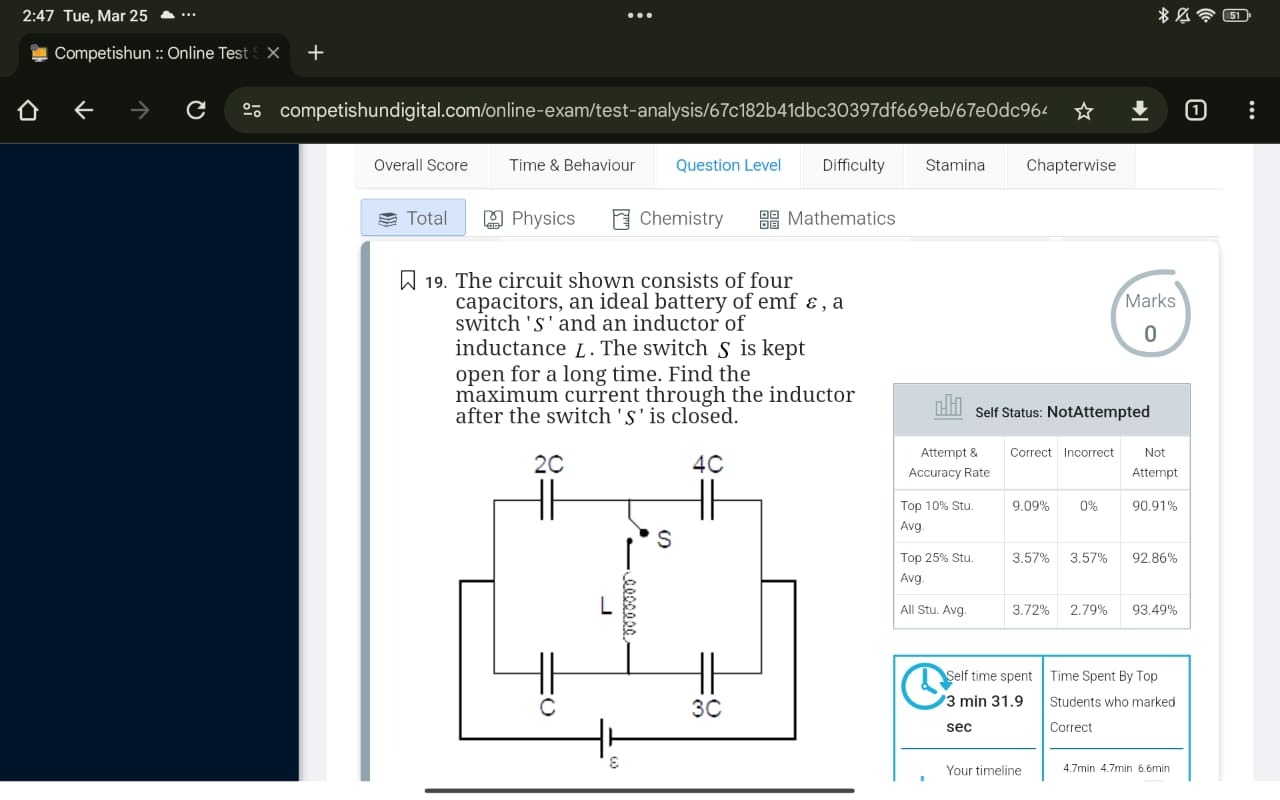
The circuit shown consists of four capacitors, an ideal battery of emf $\epsilon$, a switch 'S' and an inductor of inductance $L$. The switch $S$ is kept open for a long time. Find the maximum current through the inductor after the switch 'S' is closed.

• A. $\epsilon\sqrt{\frac{C}{L}}$
• B. $\frac{\epsilon}{2}\sqrt{\frac{C}{L}}$
• C. $\frac{2\epsilon}{\sqrt{3}}\sqrt{\frac{C}{L}}$
• D. $\frac{\epsilon}{\sqrt{2}}\sqrt{\frac{C}{L}}$

Answer 1

Answer: (C)

$\frac{2\epsilon}{\sqrt{3}}\sqrt{\frac{C}{L}}$

Answer 2

Solution:

We note that when the switch is open (for a long time) the bottom branch (the series combination of the capacitors of capacitances C and 3C connected with the battery of emf ε) is charged to ε while the top branch (the series combination of 2C and 4C) is isolated so that its voltage remains zero. When the switch S is closed the top‐branch capacitors (which cannot change their voltage instantaneously) have zero potential difference while the bottom branch is still at ε. Thus an effective voltage ε appears across the top branch which is connected in series with the inductor L.

1. Effective Capacitance of the Top Branch:

   The 2C and 4C capacitors in series have an effective capacitance

   $$C_{\text{top}}=\frac{2C\times 4C}{2C+4C}=\frac{8C^2}{6C}=\frac{4C}{3}\,.$$

2. Energy Balance:

   Initially the top‐branch capacitor has a potential difference of ε. Its stored energy is

   $$U_{C}=\tfrac12\,C_{\text{top}}\,\epsilon^2 = \frac{1}{2}\left(\frac{4C}{3}\right)\epsilon^2\,.$$

   At the moment when the current in the inductor reaches its maximum the capacitor momentarily goes through zero voltage (all the energy is in the magnetic field of the inductor). Equate the two energies:

   $$\frac{1}{2}\,L\,I_{\text{max}}^2=\frac{1}{2}\left(\frac{4C}{3}\right)\epsilon^2\,.$$

   Canceling common factors we get:

   $$L\,I_{\text{max}}^2=\frac{4C}{3}\,\epsilon^2\,,$$

   so that

   $$I_{\text{max}}=\epsilon\sqrt{\frac{4C}{3L}}=\frac{2\epsilon}{\sqrt3}\sqrt{\frac{C}{L}}\,.$$

Explanation (Minimal):

1. Find effective capacitance of 2C and 4C in series: $C_{\rm top}=\frac{4C}{3}$.

2. Recognize that when S is closed, a voltage ε suddenly appears across the top branch.

3. Equate capacitor energy $\frac12(\frac{4C}{3})\epsilon^2$ to inductor energy $\frac12 L I_{\rm max}^2$ to get

   $$I_{\rm max}=\frac{2\epsilon}{\sqrt3}\sqrt{\frac{C}{L}}\,.$$