Question

Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let ${x_i}$ be the number on the card drawn from the ${i^{th}}$ box, $i = 1,2,3.$
The probability that ${x_1},{x_2},{x_3}$ are in an arithmetic progression is:
A) $\dfrac{9}{{105}}$
B) $\dfrac{{10}}{{105}}$
C) $\dfrac{{11}}{{105}}$
D) $\dfrac{7}{{105}}$

Answer 1

Probability of an event A, is the ratio of the number of outcomes favorable to the event, to the total number of outcomes. Event is the occurrence/ experiment whose probability has to find.
P(A) = $\dfrac{{{\text{number of favorable outcomes}}}}{{{\text{total number of outcomes}}}}$
First, you need to find the number of favorable outcomes of the given condition i.e. the three cards one from each box are in Arithmetic progression, by using combinations. Then find the total number of outcomes i.e. selecting three cards one from each box by using combinations.
An arithmetic progression (A.P.) is a sequence in which terms increase or decrease regularly by the same constant. The constant is called the common difference of A.P. This will help you to draw cases for the condition that the ${x_1},{x_2},{x_3}$ are in an arithmetic progression.
‘AND’ operations are substituted with $' \times '$, implying both are likely to happen together.
‘OR’ operations are substituted with $' + '$, implying either of the one possibility is likely to happen.
The number of combinations of $n$different things taken $r$at a time, denoted by $C\left( {n,r} \right)$ , is given by
$C\left( {n,r} \right) = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$
For example: Find a number of ways in selecting two cards from box 3 of the given question which is even.
Even cards in box 3 = 2, 4, 6
Total numbers of even card in box 3, $n$ = 3
Number of cards selecting, $r$= 2
Therefore, the number of ways or combination of selecting 2 cards which are even $C\left( {n,r} \right)$ $= C\left( {3,2} \right)$
$= \dfrac{{3!}}{{2!\left( {3 - 2} \right)!}} = \dfrac{{3!}}{{2!\left( 1 \right)!}} = \dfrac{{3 \times 2!}}{{2!\left( 1 \right)}} = 3$

Complete step-by-step answer:
Step 1: Find the condition for which ${x_1},{x_2},{x_3}$ are in A.P.

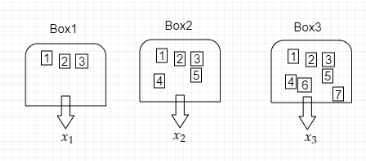
Diagram: Pictorial representation of the question.
Given that ${x_1}$ card is drawn from box 1.
${x_2}$ the card is drawn from box 1.
${x_3}$ the card is drawn from box 1.
For ${x_1},{x_2},{x_3}$ to be in Arithmetic Progression or A.P.
${x_2} - {x_1} = d$
And ${x_3} - {x_2} = d$
Here $d$is the common difference, which is added to the term to get the next term.
Therefore, ${x_2} - {x_1} = {x_3} - {x_2}$
$\Rightarrow 2{x_2} = {x_1} + {x_3}$
The term $2{x_2}$ is always even for any value of ${x_2}$.
Therefore, the sum ${x_1} + {x_3}$ must be even.
The condition ${x_1},{x_2},{x_3}$ to be in Arithmetic Progression is the sum ${x_1} + {x_3}$ should be even.
Step 2: Find the number of ways in which the sum ${x_1} + {x_3}$ is even
The sum ${x_1} + {x_3}$ is even when either ${x_1}$and ${x_3}$ both are even or ${x_1}$and ${x_3}$ both are odd.
Number of ways (or combination) in which ${x_1},{x_3}$are selected so that the sum ${x_1} + {x_3}$is even

$$= ({\text{combination of }}{x_1}{\text{is even}}) \times \left( {{\text{combination of }}{x_2}{\text{is even}}} \right) + \\\ {\text{ }}({\text{combination of}}{x_1}{\text{is odd}}) \times \left( {{\text{combination of }}{x_2}{\text{is odd}}} \right) \\\$$

$= C\left( {1,1} \right) \times C\left( {3,1} \right) + C\left( {2,1} \right) \times C\left( {4,1} \right)$
Calculate the combinations using the formula: $C\left( {n,r} \right) = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$
$= \dfrac{{1!}}{{1!\left( {1 - 1} \right)!}} \times \dfrac{{3!}}{{1!\left( {3 - 1} \right)!}} + \dfrac{{2!}}{{1!\left( {2 - 1} \right)!}} \times \dfrac{{4!}}{{1!\left( {4 - 1} \right)!}}$
$= \dfrac{{1!}}{{1!\left( 0 \right)!}} \times \dfrac{{3!}}{{1!\left( 2 \right)!}} + \dfrac{{2!}}{{1!\left( 1 \right)!}} \times \dfrac{{4!}}{{1!\left( 3 \right)!}}$
The factorial $n! = n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ...... \times 3 \times 2 \times 1$. Expand the factorial and solve it further.
$= \dfrac{1}{{1\left( 1 \right)}} \times \dfrac{{3 \times 2!}}{{1\left( 2 \right)!}} + \dfrac{{2 \times 1!}}{{1\left( 1 \right)!}} \times \dfrac{{4 \times 3!}}{{1\left( 3 \right)!}}$
$= 1 \times 3 + 2 \times 4$
$= 11$
Thus, the number of ways in which the sum ${x_1} + {x_3}$is even is 11.
Thus, the number of ways in which the ${x_1},{x_2},{x_3}$ is in Arithmetic Progression is also 11.

Step 3: Find the total number of ways of selecting ${x_1},{x_2},{x_3}$ cards one from each box.
Total number of ways (or combination) in which three cards ${x_1},{x_2},{x_3}$ can be selected from box 1, box 2, and box 3 respectively

$$= \left( {{\text{combination of one card }}{{\text{x}}_1}{\text{ sellected from box1}}} \right) \times \left( {{\text{combination of one card }}{{\text{x}}_2}{\text{ sellected from box2}}} \right) \times \\\ {\text{ }}\left( {{\text{combination of one card }}{{\text{x}}_3}{\text{ sellected from box3}}} \right) \\\$$

$= C(3,1) \times C\left( {5,1} \right) \times C\left( {7,1} \right)$
Calculate the combinations using the formula: $C\left( {n,r} \right) = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$
$= \dfrac{{3!}}{{1!\left( {3 - 1} \right)!}} \times \dfrac{{5!}}{{1!\left( {5 - 1} \right)!}} \times \dfrac{{7!}}{{1!\left( {7 - 1} \right)!}}$
$= \dfrac{{3!}}{{1!\left( 2 \right)!}} \times \dfrac{{5!}}{{1!\left( 4 \right)!}} \times \dfrac{{7!}}{{1!\left( 6 \right)!}}$
The factorial $n! = n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ...... \times 3 \times 2 \times 1$. Expand the factorial and solve it further.
$= \dfrac{{3 \times 2!}}{{1\left( 2 \right)!}} \times \dfrac{{5 \times 4!}}{{1\left( 4 \right)!}} \times \dfrac{{7 \times 6!}}{{1\left( 6 \right)!}}$
$= 3 \times 5 \times 7$
$= 105$
Thus, the total number of ways in which three cards ${x_1},{x_2},{x_3}$ can be selected from box 1, box 2, and box 3 respectively is 105.
Step 4: Find the required probability.
Probability ( ${x_1},{x_2},{x_3}$ in A.P) $= \dfrac{{{\text{number of favorable outcomes}}}}{{{\text{total number of outcomes}}}}$
$= \dfrac{{{\text{number of ways }}{{\text{x}}_1}{\text{,}}{{\text{x}}_2}{\text{,}}{{\text{x}}_3}{\text{ cards are in A}}{\text{.P}}{\text{.}}}}{{{\text{total number of ways }}{{\text{x}}_1}{\text{,}}{{\text{x}}_2}{\text{,}}{{\text{x}}_3}{\text{ cards are selected }}}}$
$= \dfrac{{11}}{{105}}$
The probability that ${x_1},{x_2},{x_3}$ are in an arithmetic progression is $\dfrac{{11}}{{105}}$ .

Thus the correct option is (C).

Note: The probability of any event is always “greater than and equal to 0” and “less than and equal to 1”.
The set of all possible outcomes is called the sample space, S of the experiment. Any subset E of sample space S is called an event. The probability of an event, E is given by:
P(E) = $\dfrac{{n(E)}}{{n(S)}}$
Where $n(E)$is the number of elements in set E, $n(S)$is the number of elements in the set S.
The first term of A.P. is denoted by $a$ , the common difference by $d$ and the last term by $l$.
The general term or ${n^{th}}$ of the A.P is ${a_n} = a + \left( {n - 1} \right)d$.