Question
Question: Both the strings shown in the figure are made of the same material and have the same cross-section. ...
Both the strings shown in the figure are made of the same material and have the same cross-section. The pulleys are light. The wave speed of a transverse wave in the string AB is v1 and in CD it is v2. The v2v1 is
A. 1
B. 2
C. 2
D. 21
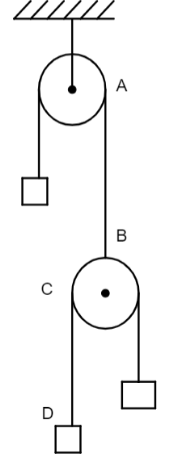
Solution
Learn the relation of velocity with the tension in the string when the system is at equilibrium. From the relation find the ratio of the velocities of the wave. The velocity of the transverse wave is proportional to the square root of the tension in the string.
Formula used:
The relation between the wave velocity and the tension in the string is given by,
v=μT
where μ is some constant that depends on the material of the wire, v is the velocity of the transverse wave and T is the tension in the string.
Complete step by step answer:
In the following system given we can see that from the image is that the tension in the string AB is twice the tension in the CD.
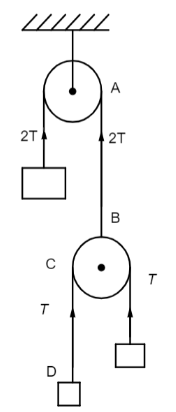
Now, the relation between the wave velocity and the tension in the string is given by,
v=μT
So, let the tension in the string CD is T so tension in the string AB will be 2T. Since all the string are made of same material, hence for string AB we can write,
v1=μ2T
And for string CD we can write, v2=μT
Hence, taking the ratio of the velocities we will have,
v2v1=μTμ2T
∴v2v1=2
Hence, the ratio of the velocities are 2.
Hence, option C is the correct answer.
Note: If the material of the strings are different then the coefficients will be different for each of the velocities. Also, this law is only valid when the system is in equilibrium else we cannot apply this law directly to any system. For that, we have to find the equilibrium condition then apply the law to find the velocity of the wave.
