Solveeit Logo
Login

Question

Question: Bong walks \( 100 \) m due North and then \( 150 \) m in a direction N \( {37^ \circ } \) E. How far...

Bong walks 100100 m due North and then 150150 m in a direction N 37∘{37^ \circ } E. How far is Bong from his original position?

Explanation

Solution

Hint : We are given that there is a person Bong who walks 100100 m in the North direction and then turns 37∘{37^ \circ } towards East and walks 150150 m. We have to find how far he currently is from the starting point. In this question, first try to draw a rough diagram to get the proper idea of what we have to calculate and then try to apply the Law of Cosines i.e.,
a2=b2+c2−2bccos⁡A b2=a2+c2−2accos⁡B c2=a2+b2−2abcos⁡C   {a^2} = {b^2} + {c^2} - 2bc\cos A \\\ {b^2} = {a^2} + {c^2} - 2ac\cos B \\\ {c^2} = {a^2} + {b^2} - 2ab\cos C \;

Complete step by step solution:
(i)
According to the given information in the question, we will first draw a rough diagram describing the route Bong took while walking.
So, first we will mark the starting point as A. Then he walked 100100 m in the North and reached a point we will name as B. Then he turned 37∘{37^ \circ } towards East and walked 150150 m and reached his final destination which we will name as C.

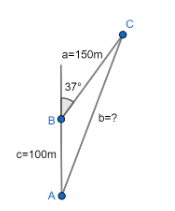
So, this is the diagram we obtained.
(ii)
In the drawn diagram we have a triangle △ABC\vartriangle ABC whose sides are as follows:
a=150 c=100   a = 150 \\\ c = 100 \;
And bb is unknown. In order to obtain the length of side bb , we will apply the law of cosines.
a2=b2+c2−2bccos⁡A b2=a2+c2−2accos⁡B c2=a2+b2−2abcos⁡C   {a^2} = {b^2} + {c^2} - 2bc\cos A \\\ {b^2} = {a^2} + {c^2} - 2ac\cos B \\\ {c^2} = {a^2} + {b^2} - 2ab\cos C \;
Since, we want the value of bb , we will use the second formula i.e.,
b2=a2+c2−2accos⁡B{b^2} = {a^2} + {c^2} - 2ac\cos B
We know that a=150a = 150 , c=100c = 100 and ∠B=180−37=143∘\angle B = 180 - 37 = {143^ \circ }
So, putting the values in the formula b2=a2+c2−2accos⁡B{b^2} = {a^2} + {c^2} - 2ac\cos B we will get:
b2=(150)2+(100)2−2(150)(100)cos⁡143{b^2} = {\left( {150} \right)^2} + {\left( {100} \right)^2} - 2\left( {150} \right)\left( {100} \right)\cos 143
(iii)
Solving the above equation, we will get:
b2=22500+10000−30000(−0.798) b2=22500+10000+23940 b2=56440 b=56440 b=237.571   {b^2} = 22500 + 10000 - 30000\left( { - 0.798} \right) \\\ {b^2} = 22500 + 10000 + 23940 \\\ {b^2} = 56440 \\\ b = \sqrt {56440} \\\ b = 237.571 \;
Since, bb is the shortest distance from the starting point to the final destination, we can say that Bong is 237.571237.571 m away from his original position.
So, the correct answer is “ 237.571m237.571 m ”.

Note : While drawing the diagram, we need to keep in mind that we are mentioning the correct directions and that 37∘{37^ \circ } turn is from the vertical line. But, ∠B\angle B here is the inner angle of the triangle and thus, we needed to subtract 37∘{37^ \circ } from 180180 in order to find ∠B\angle B . In the calculation, we need to be careful to prevent small mistakes.