Question

Bond order of $\text{B}{{\text{e}}_{\text{2}}}$ is
A. 1
B. 2
C. 3
D. 0

Answer 1

According to the molecular orbital theory, the bond order is defined as the number of covalent bonds in a molecule. Bond order is equal to half of the difference between the number of electrons in bonding (${{N}_{b}}$) and antibonding molecular orbitals (${{N}_{a}}$).

Complete Solution :
$\text{B}{{\text{e}}_{\text{2}}}$ molecule will be formed by the overlapping of atomic orbitals of two beryllium atoms.
A Be atom has four electrons. It has two valence electrons and its electronic configuration is $1{{s}^{2}}2{{s}^{2}}$. Therefore, $\text{B}{{\text{e}}_{\text{2}}}$ molecule has eight electrons which are to be filled in four molecular orbitals.

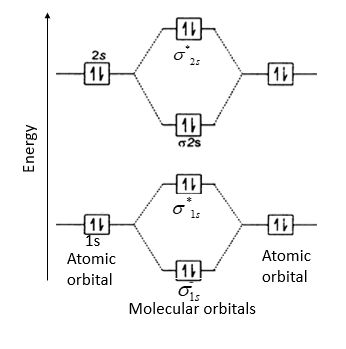
Thus, electronic configuration of $\text{B}{{\text{e}}_{\text{2}}}$ is ${{\left( \sigma 1s \right)}^{2}}{{\left( {{\sigma }^{*}}1s \right)}^{2}}{{\left( \sigma 2s \right)}^{2}}{{\left( {{\sigma }^{*}}2s \right)}^{2}}$
Here, bonding electrons, ${{N}_{b}}$ = 4 and anti-bonding electrons, ${{N}_{a}}$= 4
Therefore, bond order (B.O.) of $\text{B}{{\text{e}}_{\text{2}}}$ molecule is

& \text{B}\text{.O}\text{.=}\frac{1}{2}({{N}_{b}}-{{N}_{a}}) \\\ & \text{B}\text{.O}\text{.}=\frac{1}{2}(4-4)=0 \\\ \end{aligned}$$ \- Zero value of bond order corresponds to non-existence of $$\text{B}{{\text{e}}_{\text{2}}}$$ molecule. **So, the correct answer is “Option D”.** **Note:** The bond order of a molecule conveys the following information: 1\. The stability of a molecule can also be expressed in terms of bond order. Higher the bond order, more stable is the molecule. 2\. Bond length: Bond order and bond length are inversely related. Thus, higher the bond order, shorter is the bond length and vice-versa. 3\. Bond dissociation energy: Bond order in a molecule is directly proportional to its bond dissociation energy. Greater the bond order, more will be the value of bond dissociation energy.