Question
Question: Body diagonal of a cube is 866 pm. Its edge length would be: (A) 408 pm (B) 1000 pm (C) 500 p...
Body diagonal of a cube is 866 pm. Its edge length would be:
(A) 408 pm
(B) 1000 pm
(C) 500 pm
(D) 600 pm
Explanation
Solution
In geometry a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face.
Write the relationship between the body diagonal ‘d’ and the edge length ‘a’ of a cube:
d = 3×a
Complete answer:
Consider the right angled triangle marked with blue colour,
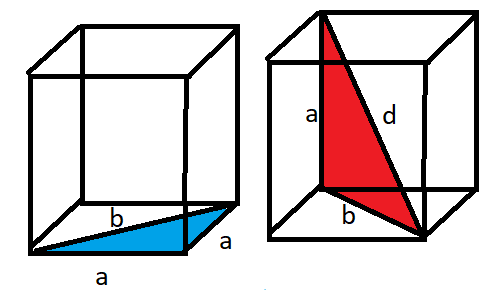
Apply Pythagoras theorem and calculate the length of the hypotenuse.
