Question

Block of mass $10kg$ is moving on an inclined plane with constant velocity $10m/s$. The coefficient of kinetic friction between the incline plane and block is:

A.$0.57$
B.$0.75$
C.$0.5$
D.None of these

Answer 1

If a system is moving at a constant velocity, then it means that the acceleration acting on the system is zero since there is no change in the velocity. Also, the net force acting on the system is equal to zero. Also, we can say that the system is in equilibrium. Therefore, we can say that the forces along the inclined plane must be equal. Using this concept, we can solve the above problem.

Complete answer:
Given the mass of the block is $m = 10kg$
The velocity with which the block is moving is given by, $v = 10m/s$
Now we can draw a free body diagram of the block,

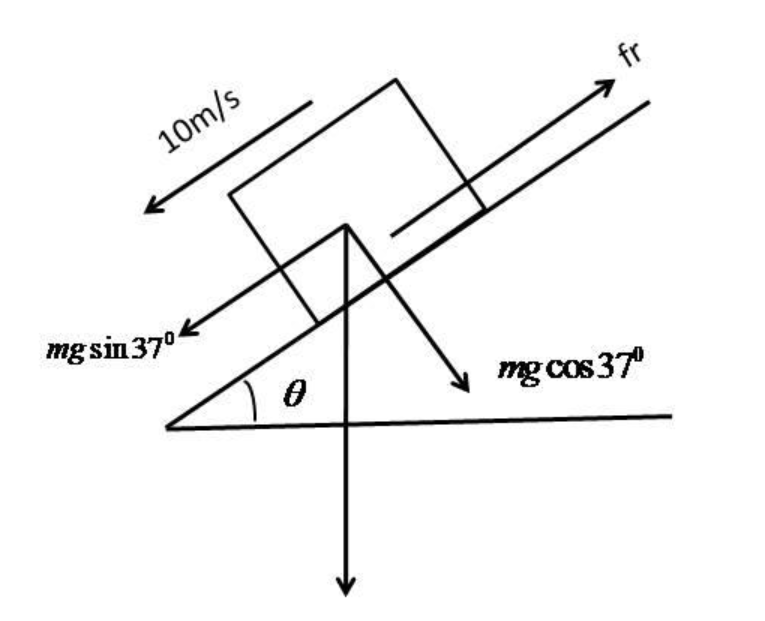
Now from the diagram, we can see the component of weight along the plane $= mg\sin {37^0}$
The component of the weight that is perpendicular to the plane is given by$= mg\cos {37^0}$. This is also the normal force acting on the block which can be represented as N.
The frictional force is acting along the plane in the opposite direction to the motion of the block. The formula for the frictional force is given as,
${f_r} = \mu N$ ……. (1)
Here,
$\mu$ is said to be the coefficient of the kinetic friction
$N$ is said to be the normal force acting on the plane.
We already said that since the system is in equilibrium forces acting along the inclined plane are equal. Here forces acting along the inclined plane are frictional force and the component of weight along the plane. Therefore equating these two equations get,
$\mu N = mg\sin {37^0}$ …… (2)
We already mentioned that the component of the weight that is perpendicular to the plane is the normal force that is represented as N. Therefore substituting this component of the weight that is perpendicular to the plane in the above equation we get,
$\Rightarrow \mu \times mg\cos {37^0} = mg\sin {37^0}$
$\Rightarrow \mu = \dfrac{{mg\sin {{37}^0}}}{{mg\cos {{37}^0}}}$
Cancel out the common terms,
$\Rightarrow \mu = \dfrac{{\sin {{37}^0}}}{{\cos {{37}^0}}}$
$\Rightarrow \mu = \tan {37^0}$
$\Rightarrow \mu = \dfrac{4}{3} = 0.75$
Therefore, the value coefficient of the kinetic friction between the block and the inclined plane is found to be $0.75$.

Hence the correct option is B.

Note:
The value that shows the relationship between any two objects that are in contact with each other and the normal reaction between the objects involved is called the coefficient of friction. This coefficient of friction value depends on the objects that are causing friction. This value normally lies between $0$ and $1$. But this value never exceeds $1$.