Question
Question: Block B is moving towards the right with constant velocity \({v_0}\). The velocity of block A with ...
Block B is moving towards the right with constant velocity v0. The velocity of block A with respect to block B is (assume all pulleys and strings are ideal):
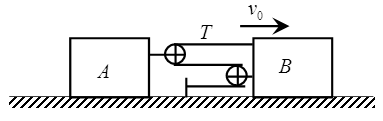
A. 2v0, left
B. 2v0, right
C. 2v03, right
D. 2v03, left
Solution
Consider the figure and take the lengths of the pulleys and a fixed point from an origin. Now take the time derivative considering the total length and the fixed point as constants. Hence we will be able to find the relative velocities of both blocks A and block B.
Complete step by step solution:
From the below figure let us consider the origin O at a suitable point. Make the coordinates of the pulleys and the fixed point concerning the origin be xA, xB, and xF.
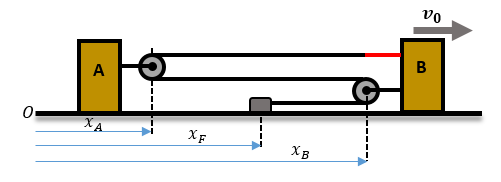
The length l of the string is then
l=(xB−xF)+2(xB−xA)=3xB−xF−2xAl=(xB−xF)+2(xB−xA)=3xB−xF−2xA
Let us disregard the little red part of the string. We can see afterward that this residual constant won't make any changes in the answer.
So however the two blocks move, the lengthlof the string continues to be constant. When the total power for the system is conserved, we can get that
The time derivative of the above equation considering l and xF are constants we get that for a constant velocity 0=dt3dxB−0−2dxA
Which implies that
3vB=2vA
Which in turn gives us,
vA=23vB
So consider that vAB=vA−vB=23vB−vB=21vB
21v0 towards the right
Hence option B is correct.
Note:
The pulleys are expected to be at rest. The tension in the string is equivalent across the pulleys as long as there is no component fixed to the string. The connection between force and acceleration is given by Newton’s second law of motion which states that acceleration of a body is directly proportional to the force utilized and it is inversely proportional to its mass.
