Question
Question: Block A of weight \(100{\text{N}}\) reset on a frictionless inclined plane of slope angle \({30^\cir...
Block A of weight 100N reset on a frictionless inclined plane of slope angle 30∘ as shown in the figure. A flexible cord attached to A passes over a frictionless pulley and is connected to a block B of weight W. Find the weight W of which the system is in equilibrium.
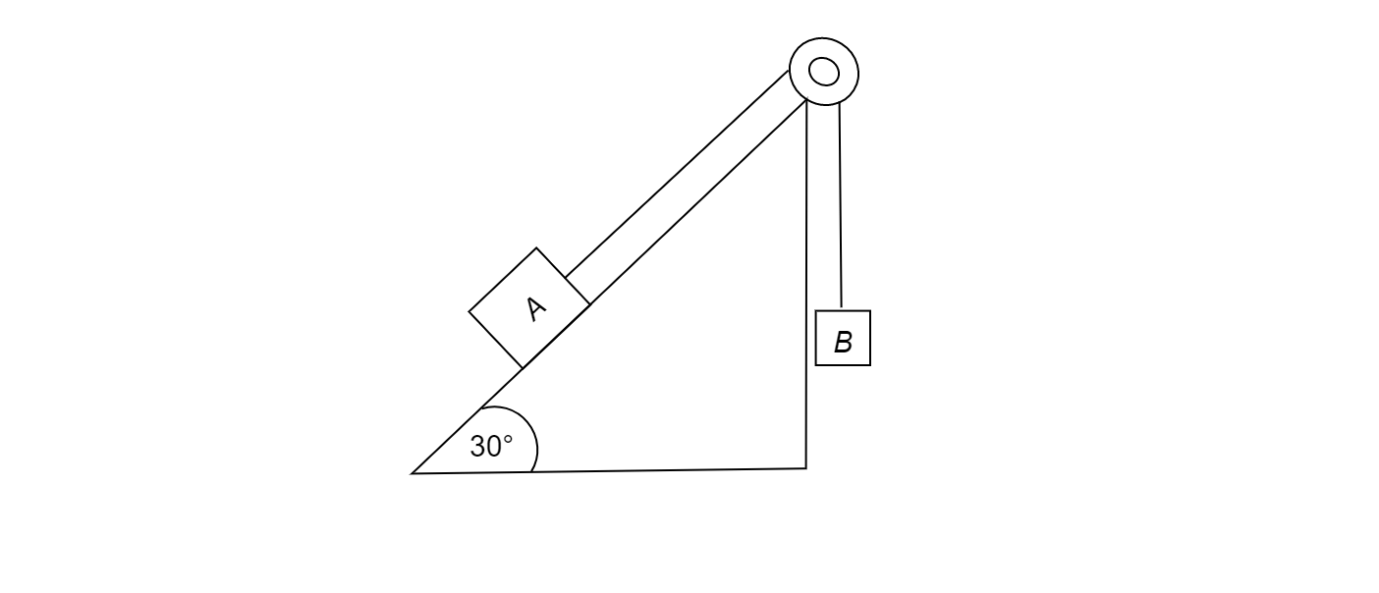
Solution
We have to know how all the forces are acting on this system at every point. We can then continue to break every force vector into its components, which will give us a better overview of this problem. After that, we will balance every force component and will try to find out our desired answer.
Complete step by step solution:
We will break every force vectors into its components and will add the tension on the string, and redraw our given figure as following-
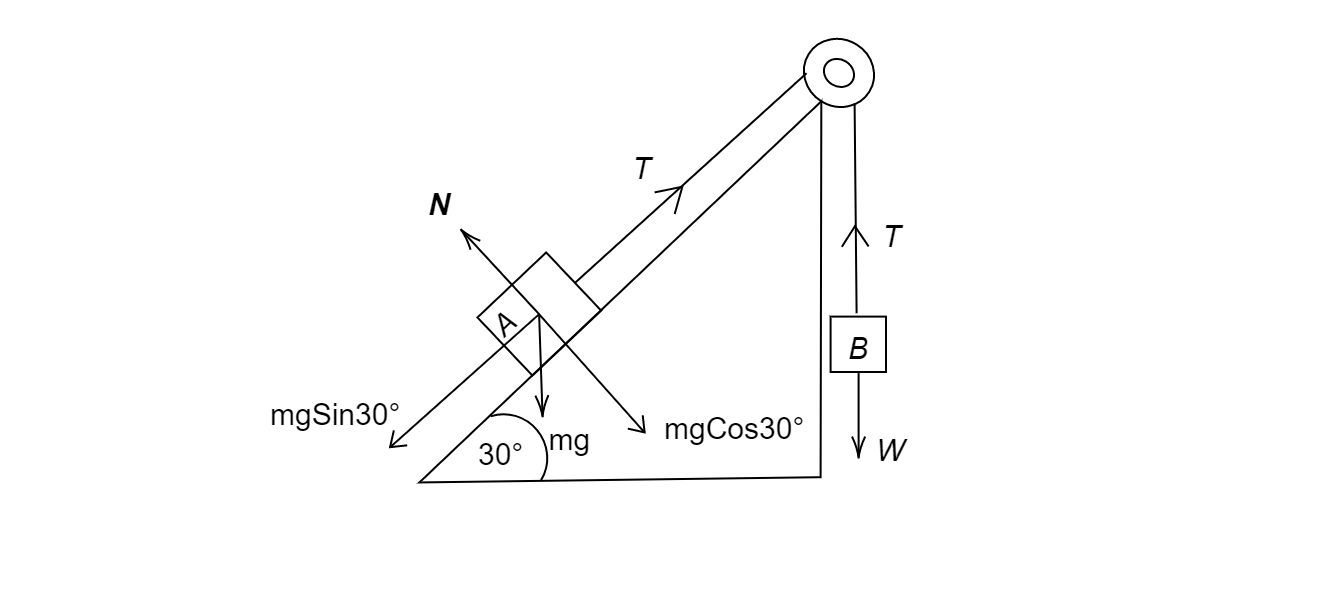
In the above figure, we have-
T is the tension in the string
W is the weight of the block B
N is the normal force acting on the block A by the surface
mg is the weight of the block A
Given that the weight of the block A is 100N i.e. mg=100N
All the forces are acting in the same direction, as shown by arrows in the figure. We break mg into its components, and we have mgcos30∘ to balance the vector N and mgsin30∘ to balance T. Also, the vector W is balancing T on the other side.
Hence in the equilibrium of the system, we have-
T=W ………..(1)
T=mgsin30∘……....(2)
By comparing equations (1) and (2), we get-
W=mgsin30∘
We put mg=100N and sin30∘=21-
∴W=100×21N
⇒W=50N
Therefore, the weight of the block B is 50N.
Note: This problem is a special case of the most generic problem. The tension at the two parts of the string is identical because the pulley and the inclined surface are frictionless. Furthermore, the sting is taken to be as massless here. In the generic problem, one must take account of the other forces that are involved.
