Question

Block A of mass m and block B of 2m are placed on a fixed triangular wedge by means of a light and inextensible and a frictionless pulley as shown in fig. The wedge is inclined at ${{45}^{\circ }}$ to the horizontal on both the sides. The coefficient of friction between block A and the wedge is $\dfrac{2}{3}$ and that between block B and the wedge is $\dfrac{1}{3}$ . If the system of A and B is released from rest, then find.
a. the acceleration of A
b. tension in the string
c. the magnitude and the direction of the frictional force acting on A?

Answer 1

In the question it is given that block A and block B are on inclined surfaces which have appreciable friction. To obtain the parameters of the motion of either blocks or tension in the string, we have to obtain the free body diagram. Further accordingly we will be able to determine the net force on each of the bodies and determine each of the parameters of the system asked in the question.

Formula used:
${{F}_{net}}=ma$

Complete answer:

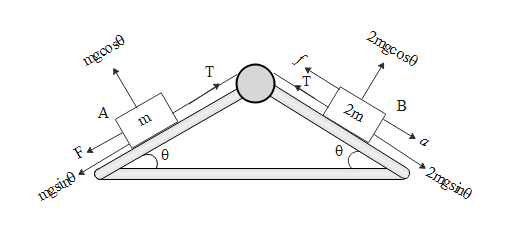
The free body diagram of the above system is shown above. The angle at which the inclined plane are inclined be $\theta ={{45}^{\circ }}$
The gravitational force i.e. product of mass times the acceleration due to gravity is vertically downwards. The components of the gravitational force are also shown in the above free body diagram. Let us say the block B with mass 2m moves downwards with acceleration ‘a’. Hence block A will move upwards as they are connected to the same string and with same acceleration as that of block B. The frictional force always opposes the motion of the body. Let the frictional force experienced by block A be ‘F and that by B be ‘f’. The frictional force is given as the product of normal force on the block times the coefficient of friction.
The net force (${{F}_{net(B)}}$ ) on block B is given by,
$\begin{aligned} & {{F}_{net(B)}}=2mg\sin \theta -f-T \\\ & \because \theta ={{45}^{\circ }},\text{ }f=\dfrac{1}{3}2mg\cos \theta \\\ & \Rightarrow 2ma=2mg\sin {{45}^{\circ }}-\dfrac{1}{3}2mg\cos {{45}^{\circ }}-T \\\ & \Rightarrow 2ma=2mg\dfrac{1}{\sqrt{2}}-\dfrac{1}{3}2mg\dfrac{1}{\sqrt{2}}-T \\\ & \therefore 2ma=\dfrac{2\sqrt{2}mg}{3}-T.....(1) \\\ \end{aligned}$
Similarly the net force(${{F}_{net(A)}}$ ) on block a
$\begin{aligned} & {{F}_{net(A)}}=T-F-mg\sin \theta \\\ & \because \theta ={{45}^{\circ }},\text{ }F=\dfrac{2}{3}mg\cos \theta \\\ & \Rightarrow ma=T-\dfrac{2}{3}mg\cos {{45}^{\circ }}-mg\sin {{45}^{\circ }} \\\ & \Rightarrow ma=T-\dfrac{2}{3}mg\dfrac{1}{\sqrt{2}}-mg\dfrac{1}{\sqrt{2}}=T-\dfrac{\sqrt{2}}{3}mg-\dfrac{\sqrt{2}}{2}mg \\\ & \therefore ma=T-\dfrac{5\sqrt{2}mg}{6}.....(2) \\\ \end{aligned}$
Adding equation 1 and two we get acceleration of block A and block B as,
$\begin{aligned} & 2ma+ma=\dfrac{2\sqrt{2}mg}{3}-T+T-\dfrac{5\sqrt{2}mg}{6} \\\ & \Rightarrow 2ma+ma=\dfrac{4\sqrt{2}mg}{6}-\dfrac{5\sqrt{2}mg}{6} \\\ & \Rightarrow 3ma=-\dfrac{\sqrt{2}mg}{6} \\\ & \therefore a=-\dfrac{\sqrt{2}g}{18} \\\ \end{aligned}$
The acceleration of B will be in the opposite direction of that taken by convention. Hence the acceleration of block A will be $\dfrac{\sqrt{2}g}{18}$ in the downward direction of itself.
Subtracting equation 1 and 2 we get the tension in the string as,
$\begin{aligned} & 2ma-ma=\dfrac{2\sqrt{2}mg}{3}-T-T+\dfrac{5\sqrt{2}mg}{6} \\\ & \Rightarrow ma=\dfrac{4\sqrt{2}mg}{6}+\dfrac{5\sqrt{2}mg}{6}-2T \\\ & \because a=-\dfrac{\sqrt{2}g}{18} \\\ & \Rightarrow m\left( -\dfrac{\sqrt{2}g}{18} \right)=\dfrac{3\sqrt{2}mg}{2}-2T \\\ & \Rightarrow -\dfrac{\sqrt{2}mg}{18}=\dfrac{3\sqrt{2}mg}{2}-2T \\\ & \Rightarrow 2T=\dfrac{\sqrt{2}mg}{18}+\dfrac{3\sqrt{2}mg}{2}=\dfrac{28\sqrt{2}mg}{18} \\\ & \therefore T=\dfrac{7\sqrt{2}mg}{9} \\\ \end{aligned}$
The frictional force acting on A is,
$\begin{aligned} & \text{ }F=\dfrac{2}{3}mg\cos \theta \\\ & \Rightarrow \text{ }F=\dfrac{2}{3}mg\cos {{45}^{\circ }}=\dfrac{2}{3}mg\dfrac{1}{\sqrt{2}} \\\ & \therefore F=\dfrac{\sqrt{2}}{3}mg \\\ \end{aligned}$
The direction of the force of friction on block A will be in the opposite direction to that of the direction taken in the free body diagram.

Note:
It is to be noted that the motion of the two blocks can be taken in any direction one wishes. The direction of motion will be determined only when the acceleration of the bodies is determined. If the acceleration is positive, then the direction of motion considered by convention is correct. But if it is negative then the motion will be in the opposite direction.