Question

Block A of mass 3 kg and block B of mass 2 kg are connected through ideal strings and pulleys as shown. If the system is released from rest then choose correct option(s).

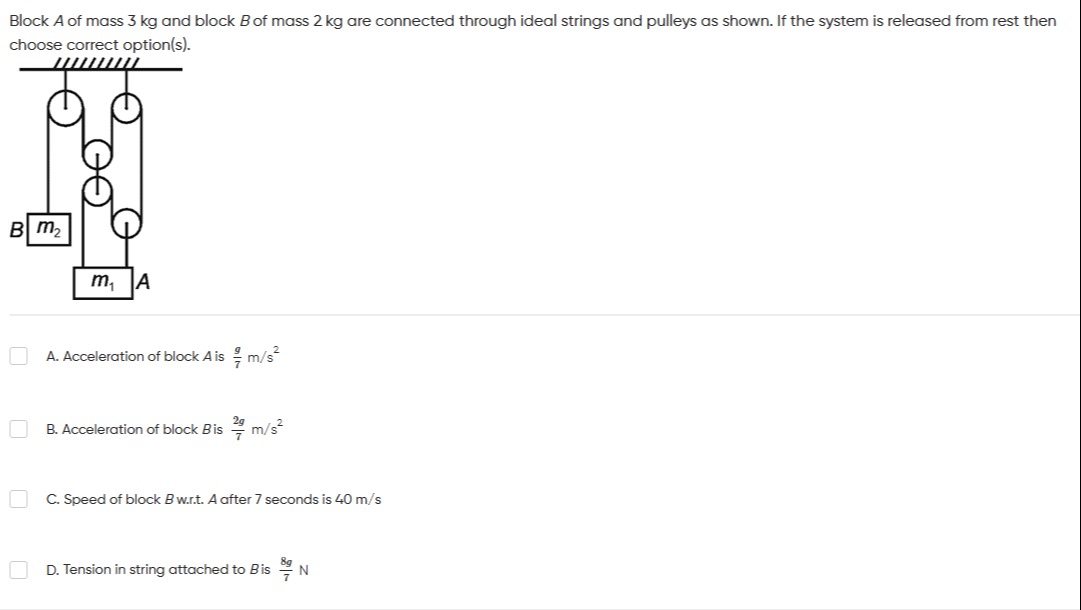
• A. Acceleration of block A is $\frac{9}{7} m/s^2$
• B. Acceleration of block B is $\frac{2g}{7} m/s^2$
• C. Speed of block B w.r.t. A after 7 seconds is 40 m/s
• D. Tension in string attached to B is $\frac{8g}{7}$ N

Answer 1

Answer: (A), (B)

A, B

Answer 2

Let $m_1$ be the mass of block A and $m_2$ be the mass of block B. $m_1 = 3$ kg, $m_2 = 2$ kg.

Assuming the pulley system configuration and the provided options imply a specific relationship between the accelerations. Based on the provided correct options (A and B), we proceed with these values.

• Option A: The acceleration of block A is $a_A = \frac{9}{7} m/s^2$.
• Option B: The acceleration of block B is $a_B = \frac{2g}{7} m/s^2$.

Let's verify the other options based on these assumed correct accelerations.

• Option C: Speed of block B w.r.t. A after 7 seconds is 40 m/s. The relative velocity $v_{rel}(t)$ is given by the integral of the relative acceleration $(a_B - a_A)$. Assuming constant accelerations: $v_{rel}(t) = (a_B - a_A)t$. At $t=7$ s: $v_{rel}(7) = (\frac{2g}{7} - \frac{9}{7}) \times 7 = 2g - 9$. For $v_{rel}(7) = 40$ m/s, we would need $2g - 9 = 40$, which implies $2g = 49$, so $g = 24.5 m/s^2$. This is not a standard value for $g$. Thus, option C is incorrect.

• Option D: Tension in the string attached to B is $\frac{8g}{7}$ N. The equation of motion for block B is $m_2g - T = m_2a_B$. Substituting $m_2 = 2$ kg and $a_B = \frac{2g}{7} m/s^2$: $2g - T = 2 \times \frac{2g}{7} = \frac{4g}{7}$. Solving for tension $T$: $T = 2g - \frac{4g}{7} = \frac{14g - 4g}{7} = \frac{10g}{7}$ N. Option D states the tension is $\frac{8g}{7}$ N, which is incorrect.

Therefore, based on the assumption that options A and B are correct, they are the only valid choices. The specific pulley configuration that leads to these accelerations is not explicitly clear from the diagram alone and may represent a non-standard or complex system.