Question

Block A is kept on smooth floor. Strings and pulleys are ideal. Find mass (in kg) of block A so that the block B moves with constant velocity.

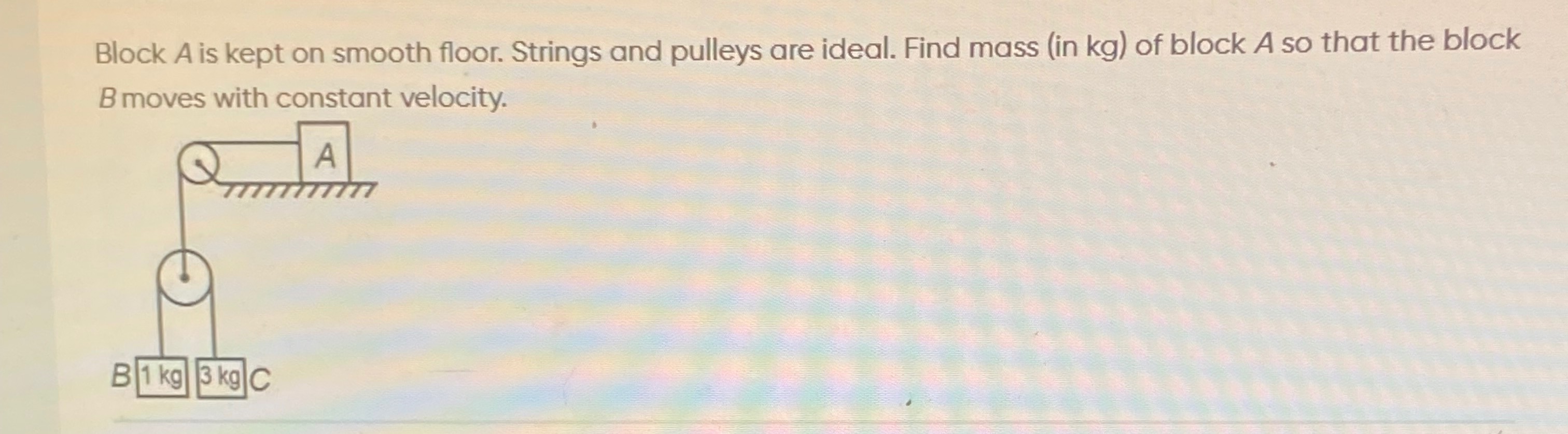
• A. 2
• B. 3
• C. 6
• D. 8

Answer 1

Answer: (C)

6 kg

Answer 2

We use the “moving‐pulley” method. Define:

• $y$: upward displacement of the movable pulley.
• $r$: extra rope length change from mass B.

Then the ground speed of mass B is $y''+r''$. For constant velocity of B,

$y''+r''=0\quad\Longrightarrow\quad r''=-y''.$

Writing Newton’s second law for masses B and C (taking downward positive):

$$\begin{array}{rcl} \text{For B:}& m_Bg -T &= m_B\,(y''+r'') = m_B\,(y''-y'')=0\quad\Longrightarrow\quad T=m_Bg,\\[1mm] \text{For C:}& m_Cg -T &= m_C\,(y''-r'')= m_C\,(y''+y'')=2m_C\,y''. \end{array}$$

Thus,

$m_Cg-T=2m_C\,y''\quad\Longrightarrow\quad 3g - (1g)=2\times3\,y''.$

So,

$2g=6\,y''\quad\Longrightarrow\quad y''=\frac{g}{3}.$

Since the movable pulley is suspended by a rope whose two segments (supporting B and C) have tension $T$, its supporting rope must have

$T_A=2T=2g.$

Block A is connected via a rope (whose length $x+(constant-y)=$ constant) so that

$x''=y''=\frac{g}{3}.$

But block A (mass $m_A$) is pulled horizontally by $T_A$; hence,

$T_A=m_A\,x''\quad\Longrightarrow\quad 2g=\;m_A\,\Bigl(\frac{g}{3}\Bigr),$

giving

$m_A=\frac{2g}{g/3}=6\text{ kg}.$