Question

The coefficient of $x^r$ in the expansion of $(1-2x)^{-1/2}$ is

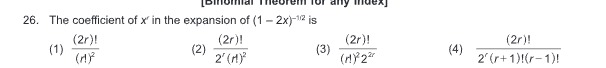
• A. (1) $\frac{(2r)!}{(r!)^2}$
• B. (2) $\frac{(2r)!}{2^r(r!)^2}$
• C. (3) $\frac{(2r)!}{(r!)^22^{2r}}$
• D. (4) $\frac{(2r)!}{2^r(r+1)!(r-1)!}$

Answer 1

Answer: (B)

$\frac{(2r)!}{2^r(r!)^2}$

Answer 2

The coefficient of $x^r$ in $(1-2x)^{-1/2}$ is given by $\binom{-1/2}{r}(-2)^r$.

We have $\binom{-1/2}{r} = \frac{(-1/2)(-1/2-1)\dots(-1/2-r+1)}{r!} = \frac{(-1/2)(-3/2)\dots(-(2r-1)/2)}{r!} = \frac{(-1)^r (1 \cdot 3 \cdot 5 \dots (2r-1))}{2^r r!}$.

The coefficient of $x^r$ is $\binom{-1/2}{r}(-2)^r = \frac{(-1)^r (1 \cdot 3 \cdot 5 \dots (2r-1))}{2^r r!} (-2)^r = \frac{1 \cdot 3 \cdot 5 \dots (2r-1)}{r!}$.

We know that $1 \cdot 3 \cdot 5 \dots (2r-1) = \frac{(2r)!}{2 \cdot 4 \cdot 6 \dots (2r)} = \frac{(2r)!}{2^r r!}$.

Substituting this back, the coefficient of $x^r$ is $\frac{1}{r!} \left( \frac{(2r)!}{2^r r!} \right) = \frac{(2r)!}{2^r (r!)^2}$.