Question
Question: Find min $U_0$ such that stone will reach other planet....
Find min U0 such that stone will reach other planet.
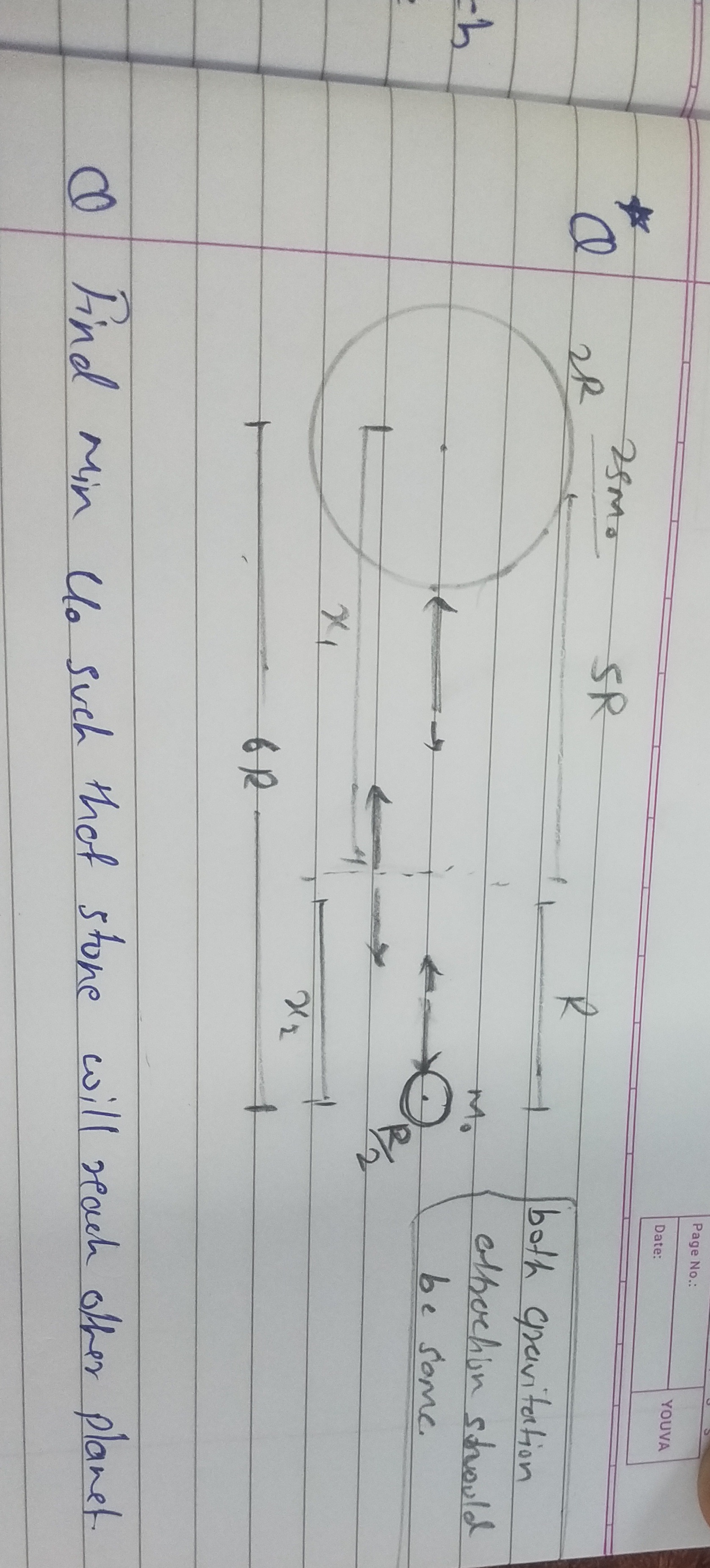
U0=12RGMm0(95−305)
Solution
The stone must have enough initial kinetic energy to overcome the gravitational potential energy barrier between the two planets. The point of unstable equilibrium, where the net gravitational force is zero, defines this barrier. Let this point be at distance rP from the center of the larger planet. The condition for zero net force is: rP2G(25M)m0=(6R−rP)2G(5M)m0 Solving for rP gives rP=23(5−5)R. The potential energy at this point is UP=−6R5GMm0(7+35). The initial potential energy on the larger planet (at r1=2R, r2=4R) is Uinitial=−455RGMm0. The minimum initial kinetic energy U0 is such that U0+Uinitial≥UP, so U0≥UP−Uinitial. U0≥12RGMm0(95−305)
