Question
Question: Find min $U_0$ such that stone will reach other planet....
Find min U0 such that stone will reach other planet.
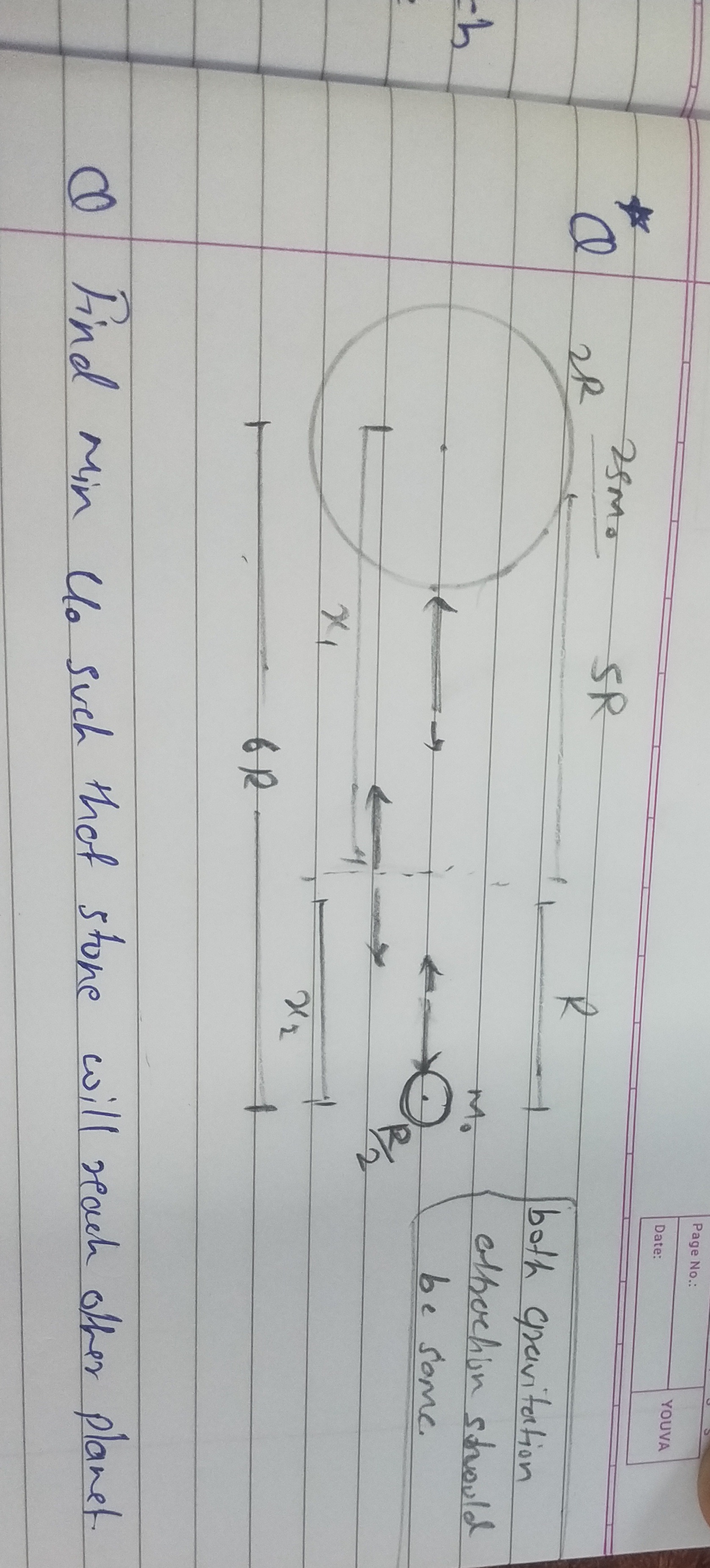
2R15GM0
Solution
The total energy of the stone is conserved. For the stone to reach the surface of the second planet, its total energy must be at least equal to the potential energy at the surface of the second planet, assuming zero kinetic energy at arrival.
Initial potential energy: Uinitial=−R1GM1m−D−R1GM2m Given M1=25M0, R1=2R, M2=5M0, R2=R, D=6R, and m=M0. Uinitial=−2RG(25M0)M0−6R−2RG(5M0)M0=−2R25GM02−4R5GM02=−4R55GM02
Final potential energy at the surface of the second planet: Ufinal=−D−R2GM1m−R2GM2m Ufinal=−6R−RG(25M0)M0−RG(5M0)M0=−5R25GM02−R5GM02=−R5GM02−R5GM02=−R10GM02
By conservation of energy (Einitial=Efinal), with Einitial=21M0U02+Uinitial and Efinal=Ufinal (minimum velocity implies zero kinetic energy at destination): 21M0U02+Uinitial=Ufinal 21M0U02=Ufinal−Uinitial 21M0U02=−R10GM02−(−4R55GM02)=4R55GM02−4R40GM02=4R15GM02 U02=4RM02×15GM02=2R15GM0 U0=2R15GM0
