Question

$\begin{vmatrix} x & x^2 & 1+px^3 \\ y & y^2 & 1+py^3 \\ z & z^2 & 1+pz^3 \end{vmatrix} = (1+pxyz)(x-y)(y-z)(z-x), \text{ where p is any scalar}$

Answer 1

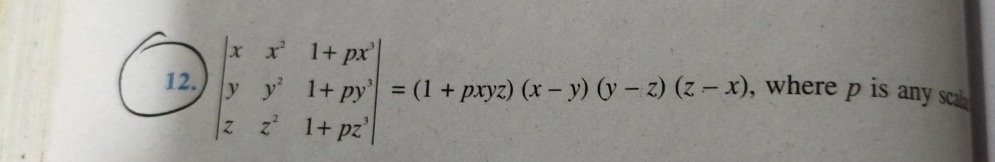
The equality holds true.

Answer 2

The given determinant is: $D = \begin{vmatrix} x & x^2 & 1+px^3 \\ y & y^2 & 1+py^3 \\ z & z^2 & 1+pz^3 \end{vmatrix}$

We can use the property of determinants that if elements of a column (or row) are expressed as a sum of two terms, the determinant can be expressed as the sum of two determinants. $D = \begin{vmatrix} x & x^2 & 1 \\ y & y^2 & 1 \\ z & z^2 & 1 \end{vmatrix} + \begin{vmatrix} x & x^2 & px^3 \\ y & y^2 & py^3 \\ z & z^2 & pz^3 \end{vmatrix}$

Let's evaluate the first determinant, $D_1$: $D_1 = \begin{vmatrix} x & x^2 & 1 \\ y & y^2 & 1 \\ z & z^2 & 1 \end{vmatrix}$ Apply row operations $R_2 \to R_2 - R_1$ and $R_3 \to R_3 - R_1$: $D_1 = \begin{vmatrix} x & x^2 & 1 \\ y-x & y^2-x^2 & 0 \\ z-x & z^2-x^2 & 0 \end{vmatrix}$ Expand along the third column: $D_1 = 1 \cdot \begin{vmatrix} y-x & y^2-x^2 \\ z-x & z^2-x^2 \end{vmatrix}$ Factor the terms in the second column: $y^2-x^2 = (y-x)(y+x)$ and $z^2-x^2 = (z-x)(z+x)$. $D_1 = \begin{vmatrix} y-x & (y-x)(y+x) \\ z-x & (z-x)(z+x) \end{vmatrix}$ Take out common factors $(y-x)$ from the first row and $(z-x)$ from the second row: $D_1 = (y-x)(z-x) \begin{vmatrix} 1 & y+x \\ 1 & z+x \end{vmatrix}$ Evaluate the $2 \times 2$ determinant: $D_1 = (y-x)(z-x) [1 \cdot (z+x) - 1 \cdot (y+x)]$ $D_1 = (y-x)(z-x) [z+x-y-x]$ $D_1 = (y-x)(z-x)(z-y)$ To match the form $(x-y)(y-z)(z-x)$, we rewrite the terms: $(y-x) = -(x-y)$ $(z-y) = -(y-z)$ So, $D_1 = (-(x-y))(z-x)(-(y-z)) = (x-y)(y-z)(z-x)$.

Now, let's evaluate the second determinant, $D_2$: $D_2 = \begin{vmatrix} x & x^2 & px^3 \\ y & y^2 & py^3 \\ z & z^2 & pz^3 \end{vmatrix}$ Take out common factor $p$ from the third column: $D_2 = p \begin{vmatrix} x & x^2 & x^3 \\ y & y^2 & y^3 \\ z & z^2 & z^3 \end{vmatrix}$ Take out common factors $x$ from the first row, $y$ from the second row, and $z$ from the third row: $D_2 = pxyz \begin{vmatrix} 1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2 \end{vmatrix}$ The remaining determinant is a Vandermonde determinant, which evaluates to $(y-x)(z-x)(z-y)$. $D_2 = pxyz (y-x)(z-x)(z-y)$ Using the same sign adjustments as for $D_1$: $D_2 = pxyz (-(x-y))(z-x)(-(y-z)) = pxyz (x-y)(y-z)(z-x)$

Finally, sum $D_1$ and $D_2$: $D = D_1 + D_2$ $D = (x-y)(y-z)(z-x) + pxyz (x-y)(y-z)(z-x)$ Factor out the common term $(x-y)(y-z)(z-x)$: $D = (1+pxyz)(x-y)(y-z)(z-x)$ This matches the given right-hand side of the equation.

The equality holds true.