Question
Question: $\begin{vmatrix} 3a & -a+b & -a+c \\ -b+a & 3b & -b+c \\ -c+a & -c+b & 3c \end{vmatrix} = 3(a+b+c)(a...
3a−b+a−c+a−a+b3b−c+b−a+c−b+c3c=3(a+b+c)(ab+bc+ca)
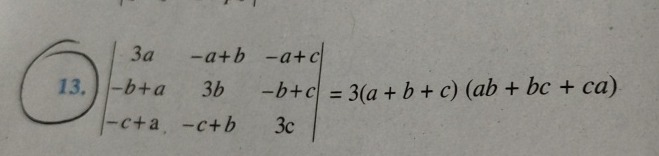
3(a+b+c)(ab+bc+ca)
Solution
To prove the given identity, we will evaluate the determinant on the left-hand side (LHS) using properties of determinants and show that it equals the expression on the right-hand side (RHS).
Let the given determinant be Δ: Δ=3a−b+a−c+a−a+b3b−c+b−a+c−b+c3c
Step 1: Apply Column Operations
Apply the operation C1→C1+C2+C3. This operation adds the elements of the second and third columns to the first column.
The new elements of the first column will be:
- For the first row: 3a+(−a+b)+(−a+c)=3a−a+b−a+c=a+b+c
- For the second row: (−b+a)+3b+(−b+c)=−b+a+3b−b+c=a+b+c
- For the third row: (−c+a)+(−c+b)+3c=−c+a−c+b+3c=a+b+c
So, the determinant becomes: Δ=a+b+ca+b+ca+b+c−a+b3b−c+b−a+c−b+c3c
Step 2: Factor out Common Term
Now, we can take out the common factor (a+b+c) from the first column: Δ=(a+b+c)111−a+b3b−c+b−a+c−b+c3c
Step 3: Apply Row Operations to Create Zeros
To simplify the determinant further, we can make two elements in the first column zero using row operations.
Apply R2→R2−R1 and R3→R3−R1.
-
For R2→R2−R1:
- 1−1=0
- 3b−(−a+b)=3b+a−b=a+2b
- (−b+c)−(−a+c)=−b+c+a−c=a−b
-
For R3→R3−R1:
- 1−1=0
- (−c+b)−(−a+b)=−c+b+a−b=a−c
- 3c−(−a+c)=3c+a−c=a+2c
The determinant now becomes: Δ=(a+b+c)100−a+ba+2ba−c−a+ca−ba+2c
Step 4: Expand the Determinant
Expand the determinant along the first column. Since the first column has two zeros, the expansion will be simple: Δ=(a+b+c)×1×a+2ba−ca−ba+2c Now, evaluate the 2×2 determinant: a+2ba−ca−ba+2c=(a+2b)(a+2c)−(a−b)(a−c) Expand the products:
- (a+2b)(a+2c)=a2+2ac+2ab+4bc
- (a−b)(a−c)=a2−ac−ab+bc
Subtract the second expansion from the first: (a2+2ac+2ab+4bc)−(a2−ac−ab+bc) =a2+2ac+2ab+4bc−a2+ac+ab−bc =(a2−a2)+(2ac+ac)+(2ab+ab)+(4bc−bc) =0+3ac+3ab+3bc =3(ab+bc+ca)
Step 5: Final Result
Substitute this back into the expression for Δ: Δ=(a+b+c)[3(ab+bc+ca)] Δ=3(a+b+c)(ab+bc+ca) This matches the RHS of the given identity.
Therefore, the identity is proven.
