Solveeit Logo
Login

Question

Question: $\begin{vmatrix} 1 & x & x^2 \\ x & x^2 & 1 \\ x^2 & 1 & x \end{vmatrix} = 3$ then value of $\begin{...

∣1xx2xx21x21x∣=3\begin{vmatrix} 1 & x & x^2 \\ x & x^2 & 1 \\ x^2 & 1 & x \end{vmatrix} = 3 then value of ∣x3−10x−x40x−x4x3−1x−x4x3−10∣\begin{vmatrix} x^3-1 & 0 & x-x^4 \\ 0 & x-x^4 & x^3-1 \\ x-x^4 & x^3-1 & 0 \end{vmatrix} is

Answer

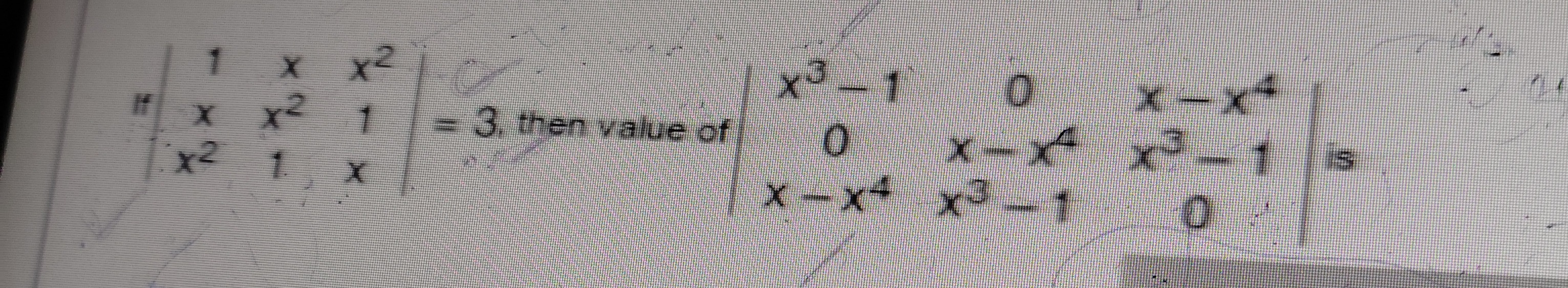
9

Explanation

Solution

Let the first determinant be D1D_1 and the second determinant be D2D_2. D1=∣1xx2xx21x21x∣D_1 = \begin{vmatrix} 1 & x & x^2 \\ x & x^2 & 1 \\ x^2 & 1 & x \end{vmatrix}

We can evaluate D1D_1 by expanding along the first row: D1=1(x2⋅x−1⋅1)−x(x⋅x−1⋅x2)+x2(x⋅1−x2⋅x2)D_1 = 1(x^2 \cdot x - 1 \cdot 1) - x(x \cdot x - 1 \cdot x^2) + x^2(x \cdot 1 - x^2 \cdot x^2) D1=(x3−1)−x(x2−x2)+x2(x−x4)D_1 = (x^3 - 1) - x(x^2 - x^2) + x^2(x - x^4) D1=x3−1−x(0)+x3−x6D_1 = x^3 - 1 - x(0) + x^3 - x^6 D1=x3−1+x3−x6=2x3−x6−1D_1 = x^3 - 1 + x^3 - x^6 = 2x^3 - x^6 - 1

Alternatively, we can use determinant properties. Apply the operation C1→C1+C2+C3C_1 \to C_1 + C_2 + C_3: D1=∣1+x+x2xx2x+x2+1x21x2+1+x1x∣=(1+x+x2)∣1xx21x2111x∣D_1 = \begin{vmatrix} 1+x+x^2 & x & x^2 \\ x+x^2+1 & x^2 & 1 \\ x^2+1+x & 1 & x \end{vmatrix} = (1+x+x^2) \begin{vmatrix} 1 & x & x^2 \\ 1 & x^2 & 1 \\ 1 & 1 & x \end{vmatrix}

Now apply R2→R2−R1R_2 \to R_2 - R_1 and R3→R3−R1R_3 \to R_3 - R_1: D1=(1+x+x2)∣1xx20x2−x1−x201−xx−x2∣D_1 = (1+x+x^2) \begin{vmatrix} 1 & x & x^2 \\ 0 & x^2-x & 1-x^2 \\ 0 & 1-x & x-x^2 \end{vmatrix}

Expand along the first column: D1=(1+x+x2)[1⋅((x2−x)(x−x2)−(1−x2)(1−x))]D_1 = (1+x+x^2) [1 \cdot ((x^2-x)(x-x^2) - (1-x^2)(1-x))] D1=(1+x+x2)[x(x−1)(−x)(x−1)−(1−x)(1+x)(1−x)]D_1 = (1+x+x^2) [x(x-1)(-x)(x-1) - (1-x)(1+x)(1-x)] D1=(1+x+x2)[−x2(x−1)2−(1−x)2(1+x)]D_1 = (1+x+x^2) [-x^2(x-1)^2 - (1-x)^2(1+x)] Since (x−1)2=(1−x)2(x-1)^2 = (1-x)^2, D1=(1+x+x2)[−(x−1)2(x2+(1+x))]D_1 = (1+x+x^2) [-(x-1)^2(x^2 + (1+x))] D1=(1+x+x2)[−(x−1)2(x2+x+1)]D_1 = (1+x+x^2) [-(x-1)^2(x^2+x+1)] D1=−(1+x+x2)2(x−1)2=−[(1+x+x2)(x−1)]2D_1 = -(1+x+x^2)^2 (x-1)^2 = -[(1+x+x^2)(x-1)]^2 Using the identity (a−b)(a2+ab+b2)=a3−b3(a-b)(a^2+ab+b^2) = a^3-b^3, we have (x−1)(x2+x+1)=x3−1(x-1)(x^2+x+1) = x^3-1. So, D1=−(x3−1)2D_1 = -(x^3-1)^2.

We are given that D1=3D_1 = 3. Therefore, −(x3−1)2=3-(x^3-1)^2 = 3, which implies (x3−1)2=−3(x^3-1)^2 = -3.

Now consider the second determinant D2D_2: D2=∣x3−10x−x40x−x4x3−1x−x4x3−10∣D_2 = \begin{vmatrix} x^3-1 & 0 & x-x^4 \\ 0 & x-x^4 & x^3-1 \\ x-x^4 & x^3-1 & 0 \end{vmatrix} Notice that x−x4=x(1−x3)=−x(x3−1)x-x^4 = x(1-x^3) = -x(x^3-1). Let A=x3−1A = x^3-1. Then x−x4=−xAx-x^4 = -xA. The determinant becomes: D2=∣A0−xA0−xAA−xAA0∣D_2 = \begin{vmatrix} A & 0 & -xA \\ 0 & -xA & A \\ -xA & A & 0 \end{vmatrix}

Expand D2D_2 along the first row: D2=A((−xA)(0)−A⋅A)−0⋅(… )+(−xA)(0⋅A−(−xA)(−xA))D_2 = A((-xA)(0) - A \cdot A) - 0 \cdot (\dots) + (-xA)(0 \cdot A - (-xA)(-xA)) D2=A(0−A2)−xA(0−x2A2)D_2 = A(0 - A^2) - xA(0 - x^2A^2) D2=−A3−xA(−x2A2)D_2 = -A^3 - xA(-x^2A^2) D2=−A3+x3A3D_2 = -A^3 + x^3A^3 D2=A3(x3−1)D_2 = A^3(x^3 - 1) Substitute A=x3−1A = x^3-1: D2=(x3−1)3(x3−1)=(x3−1)4D_2 = (x^3-1)^3 (x^3-1) = (x^3-1)^4.

We have (x3−1)2=−3(x^3-1)^2 = -3. We need to find (x3−1)4(x^3-1)^4. (x3−1)4=((x3−1)2)2=(−3)2=9(x^3-1)^4 = ((x^3-1)^2)^2 = (-3)^2 = 9.

The value of the second determinant is 9.