Question

$\begin{vmatrix} 1 & 1+p & 1+p+q \\ 2 & 3+2p & 4+3p+2q \\ 3 & 6+3p & 10+6p+3q \end{vmatrix} = 1$

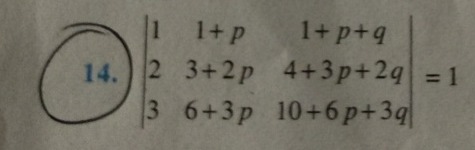
Answer 1

1

Answer 2

The determinant is simplified using elementary row operations to transform it into an upper triangular matrix.

1. $R_2 \rightarrow R_2 - 2R_1$
2. $R_3 \rightarrow R_3 - 3R_1$
3. $R_3 \rightarrow R_3 - 3R_2$

These operations result in the determinant of an upper triangular matrix:

$\begin{vmatrix} 1 & 1+p & 1+p+q \\ 0 & 1 & 2+p \\ 0 & 0 & 1 \end{vmatrix}$

The determinant of an upper triangular matrix is the product of its diagonal elements. Determinant = $1 \times 1 \times 1 = 1$.