Question
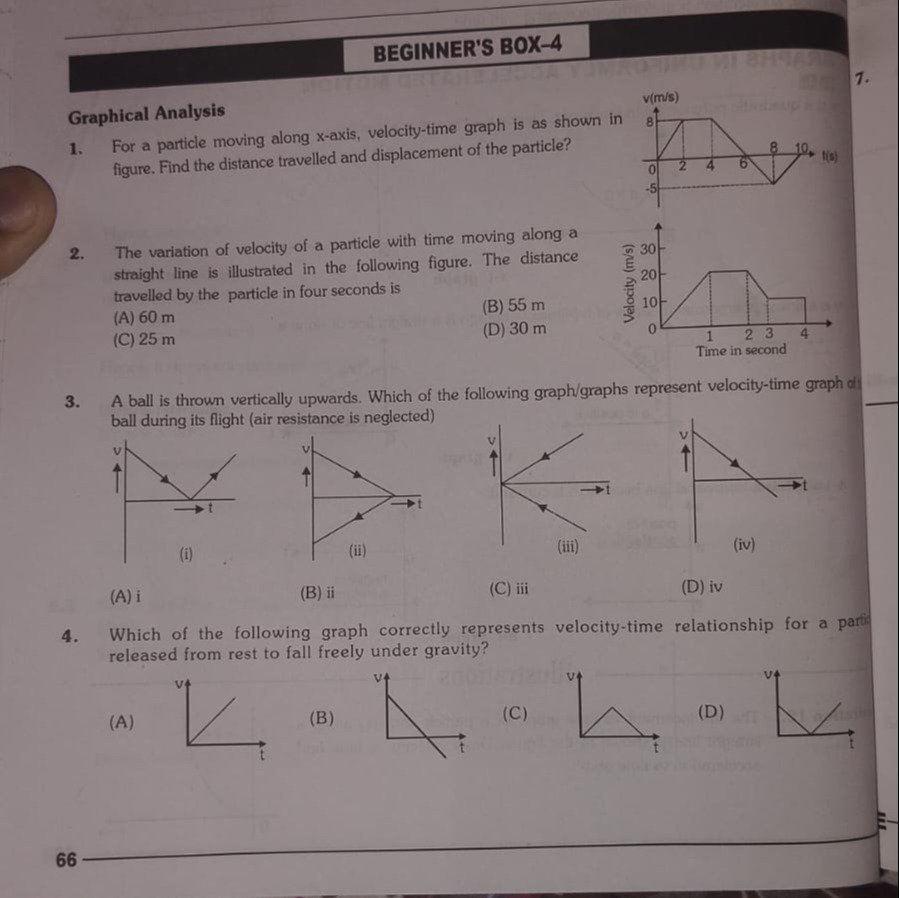
Question: For a particle moving along x-axis, velocity-time graph is as shown in figure. Find the distance tra...
For a particle moving along x-axis, velocity-time graph is as shown in figure. Find the distance travelled and displacement of the particle?
Answer
Distance travelled = 42 m, Displacement = 22 m
Explanation
Solution
-
Understanding the graph: The given graph is a velocity-time (v-t) graph.
- The area under the v-t graph represents displacement. Areas above the time axis are positive displacements, and areas below are negative displacements.
- The total distance travelled is the sum of the magnitudes of all areas.
-
Calculate areas for each segment:
- Segment 1 (0-2 s): Triangle above the t-axis. Area A1=21×base×height=21×2 s×8 m/s=8 m
- Segment 2 (2-4 s): Rectangle above the t-axis. Area A2=length×width=(4−2) s×8 m/s=2 s×8 m/s=16 m
- Segment 3 (4-6 s): Triangle above the t-axis. Area A3=21×base×height=21×(6−4) s×8 m/s=21×2 s×8 m/s=8 m
- Segment 4 (6-8 s): Triangle below the t-axis. Area A4=21×base×height=21×(8−6) s×(−5) m/s=21×2 s×(−5) m/s=−5 m
- Segment 5 (8-10 s): Triangle below the t-axis. Area A5=21×base×height=21×(10−8) s×(−5) m/s=21×2 s×(−5) m/s=−5 m
-
Calculate Total Displacement: Displacement = Sum of all areas (with sign) Δx=A1+A2+A3+A4+A5=8+16+8+(−5)+(−5)=32−10=22 m
-
Calculate Total Distance Travelled: Distance = Sum of magnitudes of all areas D=∣A1∣+∣A2∣+∣A3∣+∣A4∣+∣A5∣=8+16+8+∣−5∣+∣−5∣=8+16+8+5+5=42 m
