Question

Solve : $\log_{10}^2 x + \log_{10}x^2 = \log_{10} 3-1$

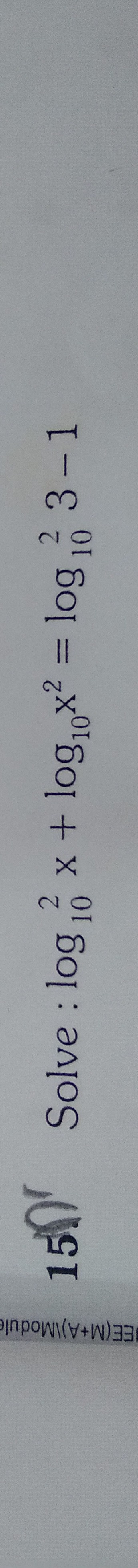
Answer 1

The solutions are $x = 10^{-1 + \sqrt{\log_{10} 3}}$ and $x = 10^{-1 - \sqrt{\log_{10} 3}}$.

Answer 2

The given equation is: $\log_{10}^2 x + \log_{10}x^2 = \log_{10} 3-1$ Using the property $\log_b a^c = c \log_b a$, we get: $(\log_{10} x)^2 + 2 \log_{10} x = \log_{10} 3 - 1$ Let $y = \log_{10} x$. The equation becomes a quadratic in $y$: $y^2 + 2y = \log_{10} 3 - 1$ Completing the square: $(y+1)^2 = \log_{10} 3$ $y+1 = \pm \sqrt{\log_{10} 3}$ $y = -1 \pm \sqrt{\log_{10} 3}$ Substituting back $y = \log_{10} x$: $\log_{10} x = -1 \pm \sqrt{\log_{10} 3}$ Exponentiating with base 10: $x = 10^{-1 \pm \sqrt{\log_{10} 3}}$ Both solutions are valid as $x>0$ is required and $10$ raised to any real power is positive.