Question

$\int (3\sqrt{x}+2)dx =$

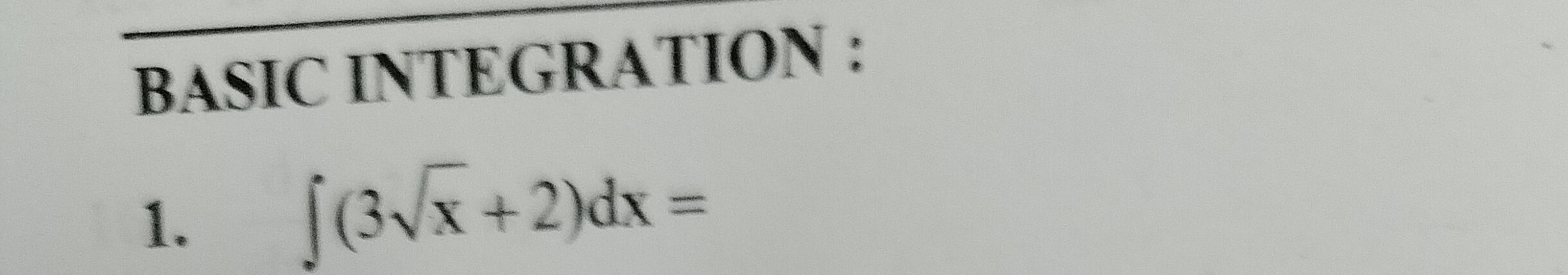
Answer 1

2x^{3/2} + 2x + C

Answer 2

The integral $\int (3\sqrt{x}+2)dx$ is evaluated by splitting it into two parts using linearity: $\int 3\sqrt{x} dx + \int 2 dx$. Constants are taken out: $3 \int x^{1/2} dx + 2 \int x^0 dx$. The power rule $\int x^n dx = \frac{x^{n+1}}{n+1} + C$ is applied to each term. $\int x^{1/2} dx = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}$ and $\int x^0 dx = \frac{x^1}{1} = x$. Substituting back and simplifying gives $3(\frac{2}{3}x^{3/2}) + 2(x) + C = 2x^{3/2} + 2x + C$.