Question

$\int (3\sqrt{x}+2)dx=$

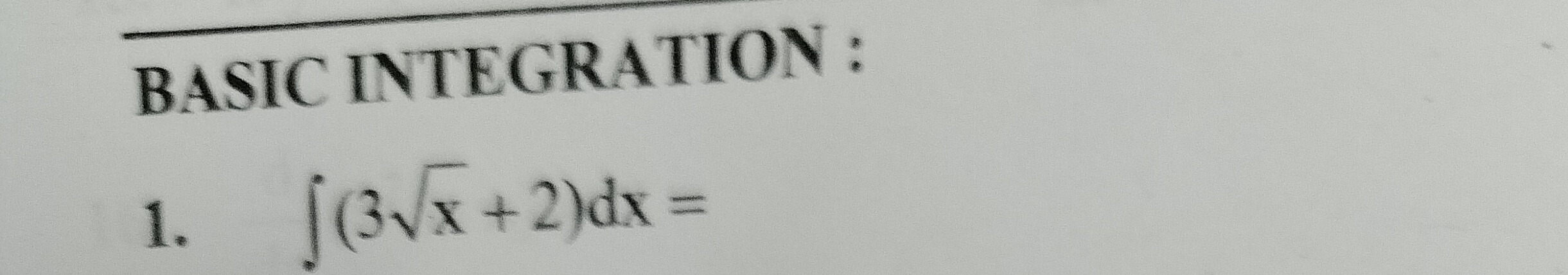
Answer 1

2x^{3/2} + 2x + C

Answer 2

Explanation of the solution:

The integral is $\int (3\sqrt{x}+2)dx$.

Using the linearity of integration, this can be split into two integrals: $\int (3\sqrt{x}+2)dx = \int 3\sqrt{x}dx + \int 2dx$.

Using the constant multiple rule, we can pull out the constants: $\int 3\sqrt{x}dx = 3 \int \sqrt{x}dx$ and $\int 2dx = 2 \int 1dx$.

Rewrite $\sqrt{x}$ as $x^{1/2}$.

Now, apply the power rule for integration, $\int x^n dx = \frac{x^{n+1}}{n+1} + C$, for $n \neq -1$.

For the first term: $3 \int x^{1/2}dx = 3 \left(\frac{x^{1/2+1}}{1/2+1}\right) + C_1 = 3 \left(\frac{x^{3/2}}{3/2}\right) + C_1 = 3 \times \frac{2}{3} x^{3/2} + C_1 = 2x^{3/2} + C_1$.

For the second term: $2 \int 1dx = 2 \int x^0 dx = 2 \left(\frac{x^{0+1}}{0+1}\right) + C_2 = 2 \left(\frac{x^1}{1}\right) + C_2 = 2x + C_2$.

Combining the results: $\int (3\sqrt{x}+2)dx = (2x^{3/2} + C_1) + (2x + C_2) = 2x^{3/2} + 2x + (C_1 + C_2)$.

Let $C = C_1 + C_2$ be the arbitrary constant of integration.

The result of the integration is $2x^{3/2} + 2x + C$.