Question

Balance the following equations by oxidation number method.
(1) $F{e_2}{O_3}\left( s \right) + CO\left( g \right) \to 2Fe\left( s \right) + 3C{O_2}\left( g \right)$
(2) $N{H_3}\left( g \right) + 5{O_2}\left( g \right) \to 4NO\left( g \right) + 6{H_2}O\left( g \right)$
(3) $K\left( s \right) + {F_2}\left( g \right) \to 2{K^ + }{F^ - }\left( s \right)$

Answer 1

In oxidation number method we need to determine the oxidation number of all atoms present. After determining the oxidation number, we will multiply the atoms that have changed by small whole numbers. By doing this we will make the total loss of electrons equal to the total gain of electrons. Then we will balance the rest of the atoms.

Complete step-by-step answer: 1. $F{e_2}{O_3}\left( s \right) + CO\left( g \right) \to 2Fe\left( s \right) + 3C{O_2}\left( g \right)$
In the first step we will assign oxidation numbers to each atom present in the equation:

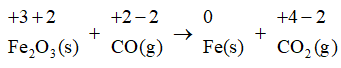
We will now identify the atoms that are being oxidized and reduced. In the above equation, the carbon atom is being oxidized since its oxidation number increases from $+ 2$ to $+ 4$ . The iron atom is being reduced since its oxidation number decreases from $+ 3$ to $0$ .
We will use a line to connect the changes in the oxidation number.

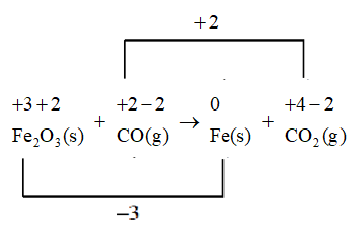
As the number of electrons lost does not equal the number of electrons gained so we will use coefficients to make the total increase in oxidation number equal to the total decrease in oxidation number.
So, the oxidation reaction should be multiplied by $3$ , while the reduction reaction should be multiplied by $2$ .
So, the correctly balanced equation will be:
$F{e_2}{O_3}\left( s \right) + 3CO\left( g \right) \to 2Fe\left( s \right) + 3C{O_2}\left( g \right)$
Here we placed $3$ in front of $CO$ and $C{O_2}$ . $2$ is placed in front of $Fe$ . $$$$

2. $N{H_3}\left( g \right) + 5{O_2}\left( g \right) \to 4NO\left( g \right) + 6{H_2}O\left( g \right)$
In the first step we will assign oxidation numbers to each atom present in the equation:

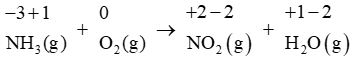
We will now identify the atoms that are being oxidized and reduced. In the above equation, the nitrogen atom is being oxidized since its oxidation number increases from $- 3$ to $+ 2$ . The oxygen atom is being reduced since its oxidation number decreases from $0$ to $- 2$ .
We will use a line to connect the changes in the oxidation number.

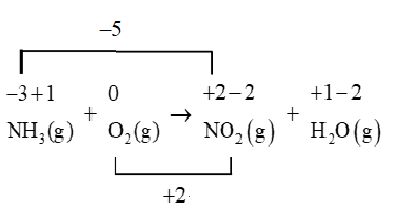
As the number of electrons lost does not equal the number of electrons gained so we will use coefficients to make the total increase in oxidation number equal to the total decrease in oxidation number.
So, the oxidation reaction should be multiplied by $2$ , while the reduction reaction should be multiplied by $5$ .
So, the correctly balanced equation will be:
$2N{H_3}\left( g \right) + 5{O_2}\left( g \right) \to 2NO\left( g \right) + 3{H_2}O\left( g \right)$
Or multiply by $2$
$4N{H_3}\left( g \right) + 5{O_2}\left( g \right) \to 4NO\left( g \right) + 6{H_2}O\left( g \right)$

3. $K\left( s \right) + {F_2}\left( g \right) \to 2{K^ + }{F^ - }\left( s \right)$
In the first step we will assign oxidation numbers to each atom present in the equation:

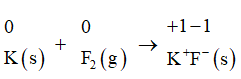
We will now identify the atoms that are being oxidized and reduced. In the above equation, the potassium atom is being oxidized from $0$ to $+ 1$ and the fluorine atom is being reduced from $0$ to $- 1$ .
We will use a line to connect the changes in the oxidation number.

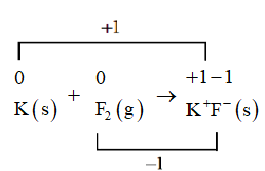
As the number of electrons lost does not equal the number of electrons gained so we will use coefficients to make the total increase in oxidation number equal to the total decrease in oxidation number.
So, the oxidation reaction should be multiplied by $2$ , while the reduction reaction is multiplied by $2$ .
So, the correctly balanced equation will be:
$2K\left( s \right) + {F_2}\left( g \right) \to 2{K^ + }{F^ - }\left( s \right)$

Note: In the first equation we do not put $2$in front of $F{e_2}{O_3}$ as it already consists of $2$in its subscript and also in the last reaction we are putting 2 in front of $K$ and ${K^ + }{F^ - }$ as fluorine already consists of $2$ in its subscript part hence we do it in order to balance the equation. The oxidation number of elements in its free uncombine state is always taken as zero. This is also true for elements found in nature as diatoms. E.g. ${H_2},{O_2},C{l_2},{F_2},{N_2}$ etc.