Solveeit Logo
Login

Question

Question: 2) If $y = tan^{-1}(secx^3 - tanx^3) \quad \pi/2 < x^3 < 3\pi/2$...

  1. If y=tan−1(secx3−tanx3)π/2<x3<3π/2y = tan^{-1}(secx^3 - tanx^3) \quad \pi/2 < x^3 < 3\pi/2
A

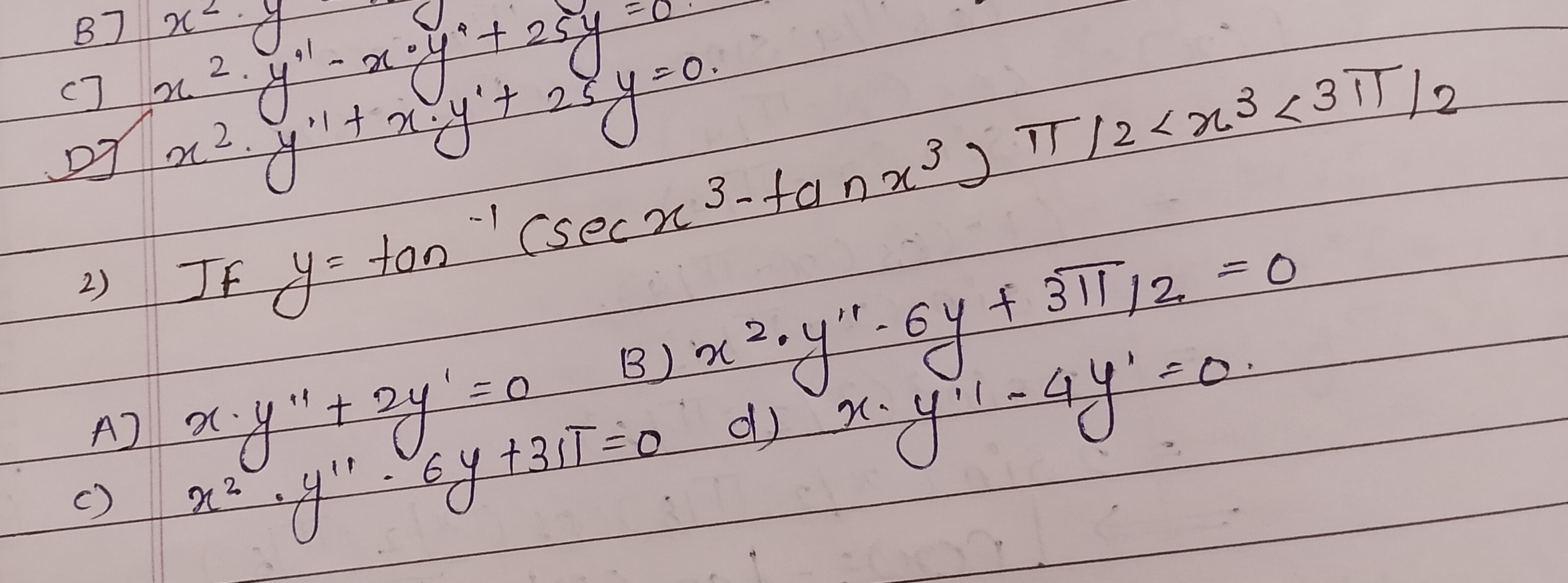
x⋅y′′+2y′=0x \cdot y'' + 2y' = 0

B

x2⋅y′′−6y+3π/12=0x^2 \cdot y'' - 6y + 3\pi/12 = 0

C

x2⋅y′′−6y+3π=0x^2 \cdot y'' - 6y + 3\pi = 0

D

x⋅y′′−4y′=0x \cdot y'' - 4y' = 0

Answer

None of the options is correct

Explanation

Solution

We are given

y=tan⁡−1(sec⁡(x3)−tan⁡(x3)),y=\tan^{-1}\Bigl(\sec(x^3)-\tan(x^3)\Bigr),

with π/2<x3<3π/2.\pi/2<x^3<3\pi/2.

A standard trig manipulation shows that

tan⁡−1(sec⁡(x3)−tan⁡(x3))=tan⁡−1(tan⁡(π4−x32))=π4−x32,\tan^{-1}\Bigl(\sec (x^3)-\tan(x^3)\Bigr) =\tan^{-1}\Bigl(\tan\Bigl(\tfrac{\pi}{4}-\tfrac{x^3}{2}\Bigr)\Bigr) =\frac{\pi}{4}-\frac{x^3}{2},

since the angle π4−x32\frac{\pi}{4}-\frac{x^3}{2} (which lies between −π/2-\pi/2 and π/2\pi/2) is in the range of the inverse‐tangent. Thus

y=π4−x32y=\frac{\pi}{4}-\frac{x^3}{2}.

A quick calculation gives

y′=−32x2,y′′=−3x.y'=-\frac{3}{2}x^2,\quad y''=-3x.

It is now a simple (but straightforward) matter to check that if we substitute these expressions into any of the four candidate equations the answer will not vanish identically. (For example, even

x y′′+2y′=x(−3x)+2(−32x2)=−3x2−3x2=−6x2x\,y''+2y' = x(-3x)+2\Bigl(-\frac{3}{2}x^2\Bigr) =-3x^2-3x^2=-6x^2

which is not identically zero.) One may check that none of options A, B, C or D leads to an identity. (In fact one easily finds that the function y=π4−x32y=\frac{\pi}{4}-\frac{x^3}{2} satisfies an equation like

y′′2+6y′=0,y''^2+6y'=0,

which is not among the given choices.)