Question
Question: If $y = tan^{-1}(secx^3 - tanx^3)$, $\pi/2 < x^3 < 3\pi/2$...
If y=tan−1(secx3−tanx3), π/2<x3<3π/2
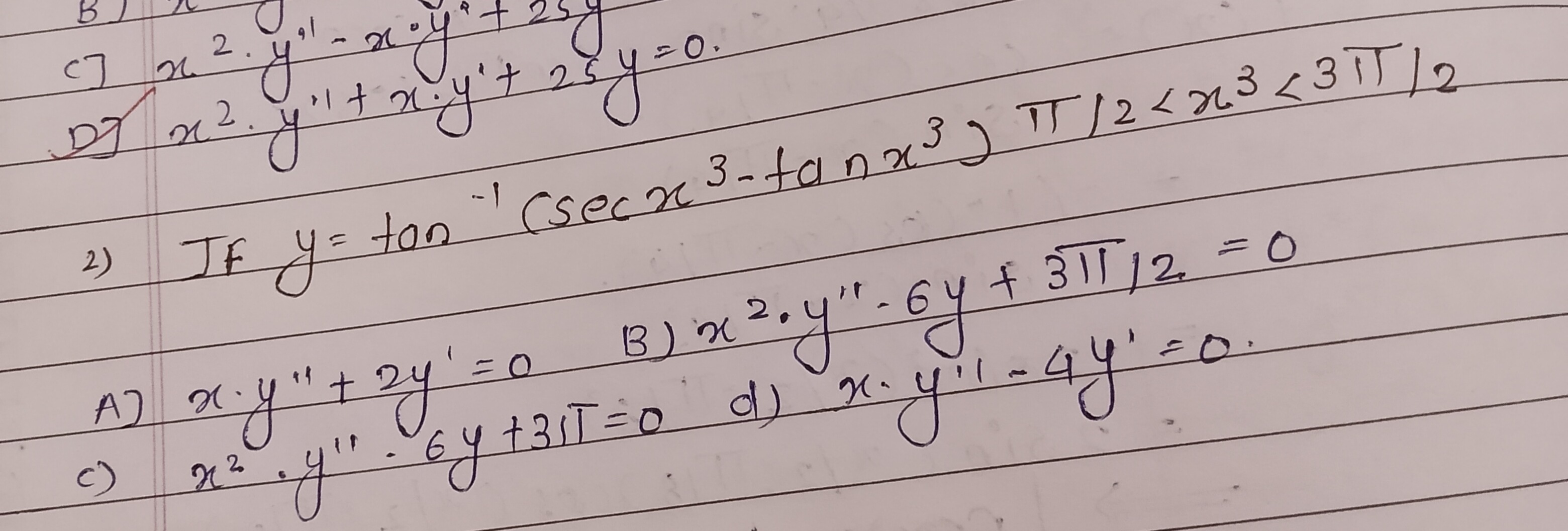
x.y′′′+2y′=0
x2.y′′−6y+123π=0
x2.y′′−6y+3π=0
x.y′′′−4y′=0.
None of the given options is correct.
Solution
We wish to “simplify”
y=tan−1(secx3–tanx3).
A standard trick is to write the expression in “sine‐cosine form”. First note that
secθ–tanθ=(1–sinθ)/cosθ.
Now with the substitution
θ=x3 (so that x3 lies between π/2 and 3π/2)
write
tany=secx3–tanx3=(1–sinx3)/cosx3.
A standard half–angle manipulation shows that
(1–sinx3)/cosx3=(1–t)/(1+t) where t=tan(x3/2).
But one may verify that
tan(π/4–x3/2)=(1–tan(x3/2))/(1+tan(x3/2))=(1–t)/(1+t).
Thus
tany=tan(π/4–x3/2)
so that (by the range of arctan)
y=π/4–x3/2.
This is an “explicit” expression for y. Being a polynomial (really a linear function of x3) it has third derivative equal to the constant
y′′′=–3.
Thus y satisfies
y′′′+3=0.
None of the options given in part (2) is equivalent to y′′′+3=0.
